Let V = {(a_n)n S | a_n = a_n1 + a_n2 for all n 2}, and let s, t V be the sequences beginning

s = (1, 0, 1, 1, 2, 3, 5, . . .)

t = (0, 1, 1, 2, 3, 5, 8, . . .)

It is a fact that B = {s, t} is a basis for V , and you may assume this fact. Now consider the linear transformation(seen in the picture below)

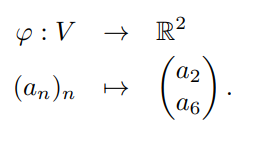
Let V = an)\" E 8 l on = on_1 + un_2 for all u Z_> 2}, and let s,t E V be the sequences beginning 8 = (1,0,1,1,2,3,5,...) t = (0,1,1,2,3,5,8,...) It is a fact that B = {3,13} is a basis for V, and you may assume this fact. Now consider the linear transformation (,0 : V > R2 (2 (Gab: I> (as) . (a) Find [go]g<_5 where e="{81,82}," the standard basis of r2. using part show that if gun and are sequences in v satis- fying b2 as="()6," then on="on" for all u hint: what does your answer to port tell you about whether is injectiue>