Question: Let w =f(u) + g(v), where u =x + iy, v=x - iy, and i = v -1. Show that w satisfies the Laplace equation
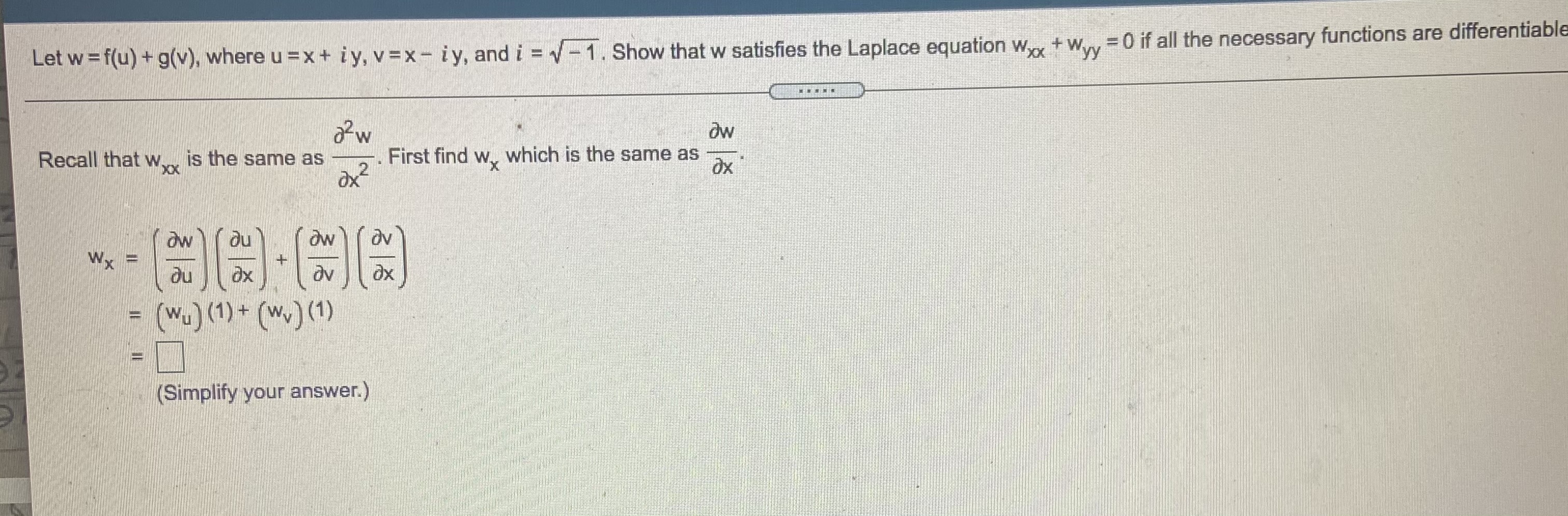
Let w =f(u) + g(v), where u =x + iy, v=x - iy, and i = v -1. Show that w satisfies the Laplace equation Wyx + Wyy =0 if all the necessary functions are differentiable 2 2 w Ow Recall that we is the same as ax 2 First find w, which is the same as ax ow Wx ax - (Wu) (1) + (wv) (1 ) = (Simplify your answer.)
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock
Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock
Study Help