Let X ₁ , . . .,X _n and Y ₁ , . . . , Y _m be independent random samples from the distributions N(? ₁ , ? ₃ ) and N(? ₂ , ? ₄ ), respectively.

(a) Show that the likelihood ratio for testing H ₀ : ? ₁ = ? ₂ , ? ₃ = ? ₄ against all alternatives is given by

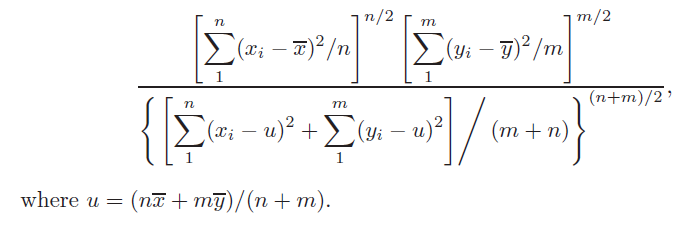
(b) ? Show that the likelihood ratio for testing H ₀ : ? ₃ = ? ₄ with ? ₁ and ? ₂ unspecified can be based on the test statistic F given in expression (8.3.8).

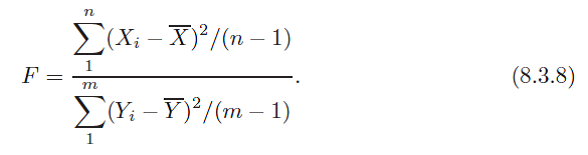
n/2 m { (2i - u)2 + (yi 1-2) / (m + n) m where u = (na + mg)/(n + m). m/2 (n+m)/2' F = n (x; - X)/(n 1) 1 m (; - Y)/(m 1) 1 (8.3.8)