Question: 1. Let X be a Banach space and let T be a bounded linear operator on X. Show that if ||T|| < 1, then

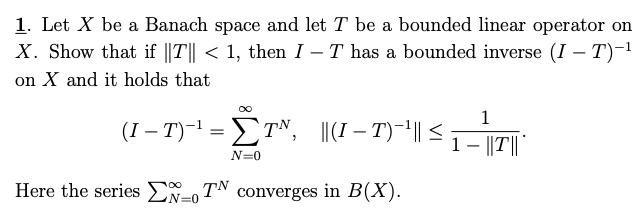
1. Let X be a Banach space and let T be a

1. Let X be a Banach space and let T be a bounded linear operator on X. Show that if ||T|| < 1, then I - T has a bounded inverse (I-T)- on X and it holds that 0 1 (I T)- = TN, ||(I - T) -`' || 1 - ||T|| | N=0 Here the series o TN converges in B(X). N=0

Step by Step Solution

★★★★★

3.34 Rating (160 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Solution let X be T let operator IT II 1 then inverse IT tha... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Finance Questions!

Let X be a linear space. Two affine subsets S and T are parallel if one is a translate of the other, that is, S = T + x for some x X Show that the relation S is parallel to T is an equivalence...

Let X be a linear space and

Let x be a normally distributed random variable having mean = 30 and standard deviation = 5. Find the z value for each of the following observed values of x: a. x = 25 b. x = 15 c. x = 30 d. x = 40...

A point object is placed at a distance of 20 cm from a thin plano-convex lens of focal length 15 cm, if the plane surface is silvered. The image will form at (A) 60 cm left of AB (C) 12 cm left of AB...

Consider a firm that has a debt-equity ratio of 1/3. The rate of return for debt is 6% and the rate of return for equity is 13%. The corporate tax rate is 32%. What is the weighted average cost of...

Functional analysis Questions 81 17:36 - Expert Q&A W + 2. A subset M of a normed space X is said to be conver if x, y e M implies that { z EX : 2 = ax + ( 1 - c ) y, 0 s as1}cM, i.e. if the "line...

ANSI-SPARC6 Programming Language Compilation Write notes on each of the following topics: (a) the implementation of labels and jumps in a recursive, block structured programming language [7 marks]...

Applied Mathematics and Computation 95 (1998) 181192 Love dynamics: The case of linear couples Sergio Rinaldi 1 Centro Teoria dei Sistemi, CNR, Politecnico di Milano, Via Ponzio 34/5, 20133 Milan,...

Show work/explanation where indicated. Answers without any work may earn little, if any, credit. You may type or write your work in your copy of the exam, or if you prefer, create a document...

Math 104A Homework #3 Instructor: Lihui Chai General Instructions: Please write your homework papers neatly. You need to turn in both full printouts of your codes and the appropriate runs you made....

(Earnings per Share) At December 31, 2003, Shiga Naoya Corporation had the following stock outstanding. 10% cumulative preferred stock, $100 par, 107,500 shares $10,750,000 Common stock, $5 par,...

How Has Poker Become Popular Amongst Lithuanians

When a critical risk issue appears that requires immediate action, describe how you would make critical decisions quickly and intuitively to manage the complex risk. What document could you refer to

Given the data below: a. Calculate the efficient frontier assuming no short sales are allowed. b. Calculate the efficient frontier assuming that short sales are allowed. c. Graph both frontiers on...

Determine the vertical rise h of the load W during 10 seconds if the hoisting drum draws in cable at the constant rate of 180 mm/s. M W Problem 2/221

In 2010, Hershey, the U.S. chocolate maker, announced plans to boost its presence in Europe. The companys best known brand is Hersheys Kisses, but other brands include Hugs and Reeses Pieces. The...

Survey the Federal Reserve Board explanations, charts, and aggregate data to form an opinion as to how important commercial paper is to the U.S. economy. Compose a paragraph summarizing your findings...

You have 10 m of 0.50-mm-diameter copper wire and a battery capable of passing 15 A through the wire. What magnetic field strengths could you obtain (a) inside a 2.0-cm-diameter solenoid wound with...

Consider the two-tailed probability value from the analysis. What is the appropriate interpretation for this value? Group of answer choices Only 2 in 1000 (.002) samples would produce an age mean...

The space BL(X, Y) of all bounded linear functions from X to Y is a normed linear space, with norm It is a Banach space (complete normed linear space) if Y is complete. The following proposition is...

In the context of solving the problem with a bottom-up dynamic programming algorithm. . . NOT NCESSARY INFORMATION (i) Give and clearly explain a formula that expresses the optimal solution in terms...

Let S be a nonempty subset of a linear space, and let m = dim S =dim aff S. Consider the set 1. Show that dim cone = dim S + 1. 2. For every x conv S, there exists m +1 points x1, x2,...,xm+1 S...

answer the question clearly You are building a flight-control system for which a convincing safety case must be made. Would you assign the tasks of safety requirements engineering, test case...

6 The Multivariate Normal Distribution The multivariate normal distribution with mean R d and positive definite covariance matrix R dd , denoted N(, ), has the probability density function f(x; , ) =...

Let (x) := x|cos(/x)| for x [0, 1] and let (0+ := 0. Then is continuous on [0, 1] and (x) exists for x E1 := {0} {ak : k N}, where ak := 2/(2k + 1). Let (x) := (x) for x E and (x) := 0 for x ...