Question: - Let (X) be a random walk such that Xo = 0, and for all n, P(Xn+1 - Xn= 1)=1/3 and P(Xn+1 - Xn

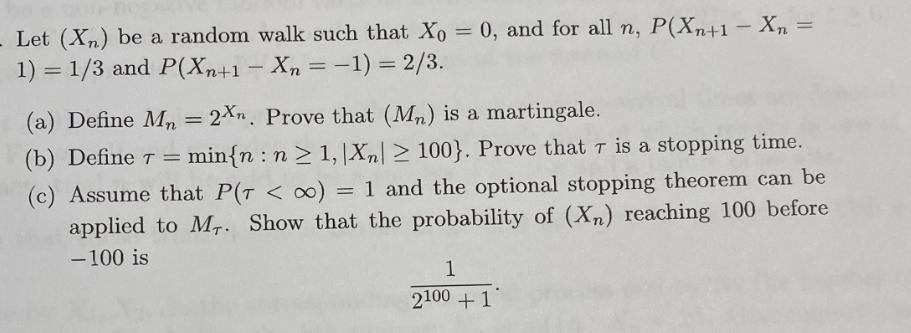
- Let (X) be a random walk such that Xo = 0, and for all n, P(Xn+1 - Xn= 1)=1/3 and P(Xn+1 - Xn = -1) = 2/3. (a) Define Mn = 2x. Prove that (Mn) is a martingale. == = (b) Define 7 = min{n: n > 1, |X| 100}. Prove that r is a stopping time. (c) Assume that P(T < ) = 1 and the optional stopping theorem can be applied to Mr. Show that the probability of (Xn) reaching 100 before -100 is 1 2100+1

Step by Step Solution

★★★★★

3.48 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Q1. You have identified a market opportunity for home media players that would cater for older members of the population. Many older people have difficulty in understanding the operating principles...

WeldOrg was recently cited for three separate violations and fined a total of $40,959, which represents the maximum penalty for each violation. Based on this, it is likely that a. two violations were...

answer the question clearly You are building a flight-control system for which a convincing safety case must be made. Would you assign the tasks of safety requirements engineering, test case...

The cash position of George's monthly investment account follow the fol- lowing random walk with initial value X1 = 20 for n > 1, Xn+1 = Xn + 8y, (in other way Xn+1 = X1 + sv;) i=1 where 3 Suppose...

Problem 1 (15 points). Consider the Binomial Asset Pricing Model, with u = 2, d = 1/2, r = 1/4 and S, = 4. Consider a European Call Option with strike price K = 9, maturing at time N = 3. (1) State...

Anna, Emma, and Ina decided to form a partnership. Their capltal accounts are as follows: Anna Date January 1 300,000 April 1 150,000 May 1 July 1 September 600,000 1 October 1 (450,000) Emma Ina...

Math 350 - Homework 3 - Solutions 1. The bus will arrive at a time that is uniformly distributed between 8 and 8 : 30 A.M. If we arrive at 8 A.M., what is the probability that we will wait between 5...

Deduce the invariant distribution. (Oxford 2005) * 14. Consider a Markov chain with state space S = {0, 1, 2, . . . } and transition matrix given by pi, j = ( qp ji+1 for i 1 and j i 1, qp j for i...

n a computerized inventory management system, all data regarding an item's identity, price, and source originates with the ____ component. A. accounts payable B. point-of-sale C. store receiving D....

+ Dejardines Financial has provided a $53,217 loan to Your Finished Inc. that earns interest at a rate of 6.5% compounded monthly. The loan is to be paid back in equal payments at the end of each...

Find P(E or F) if P(E and F) = 0.15. Find the probability of the indicated event if P(E) = 0.25 and P(F) = 0.45.

Consider the function Then, we calculate f" (a). We get: (2) - J'(x) -| Pusz We want to find its degree two Taylor polynomial T(e) near a = 7- First, we calculate f'(a). We get: 6 1 1 t 12 dt. f"(x)...

A solid wooden object turned on a lathe has a length of 5 0 cm and diameters ( measured in cm ) shown in the figure. ( A lathe is a tool that spins and cuts a block of wood so that it has circular...

What is the current through 14V battery if you replace 4 Ohm resistor by 2 Ohm and 2 Ohm resistor by 9 Ohm? Your result must contain two decimal places. Use the current directions as they are in the...

Transactions that affect longterm liabilities and stockholders equity are classified as which of the following? a. Administrative activities b. Financing activities c. Investing activities d....

Rock Solid Manufacturing, Inc., has acquired the net assets of Jelly Soft Manufacturing, Inc., for $10 million and now needs to address how the acquisition should be recorded on its books for...

The management of Graphicopy is trying to determine how much debt they should have in their capital structure. If they sell $500,000 in perpetual bonds with a 9 percent coupon, what would be the...

In developing an interval estimate for a population mean, a sample of 40 observations was used. The interval estimate was 28.76 + 1.48. Had the sample size been 160 instead of 40, the interval...

1 + ((SELECT 1 FROM (SELECT SLEEP(1))A))/*'XOR(((SELECT 1 FROM (SELECT SLEEP(1))A)))OR'|"XOR(((SELECT 1 FROM (SELECT SLEEP(1))A)))OR"*/

In Exercises determine whether the limit exists on the basis of the graph of y = (x). The domain of is the set of real numbers. lim f(x) ab

In Exercises write the inequality in the form a

In Exercises a parametrization is given for a curve. (a) Graph the curve. What are the initial and terminal points, if any? Indicate the direction in which the curve is traced. (b) Find a Cartesian...

Although some financial institutions do not charge fees for using ATMs, many do. A recent study found the average fee charged by banks to process an ATM transaction was $2.91. The file titled ATM...

Discuss the difference between discrete and continuous probability distributions. Discuss two situations in which a variable of interest may be considered either continuous or discrete.

Recall the Empirical Rule from Chapter 3. It states that if the data distribution is bell shaped, then the interval contains approximately 68% of the values, 2 s contains approximately 95%, and ...