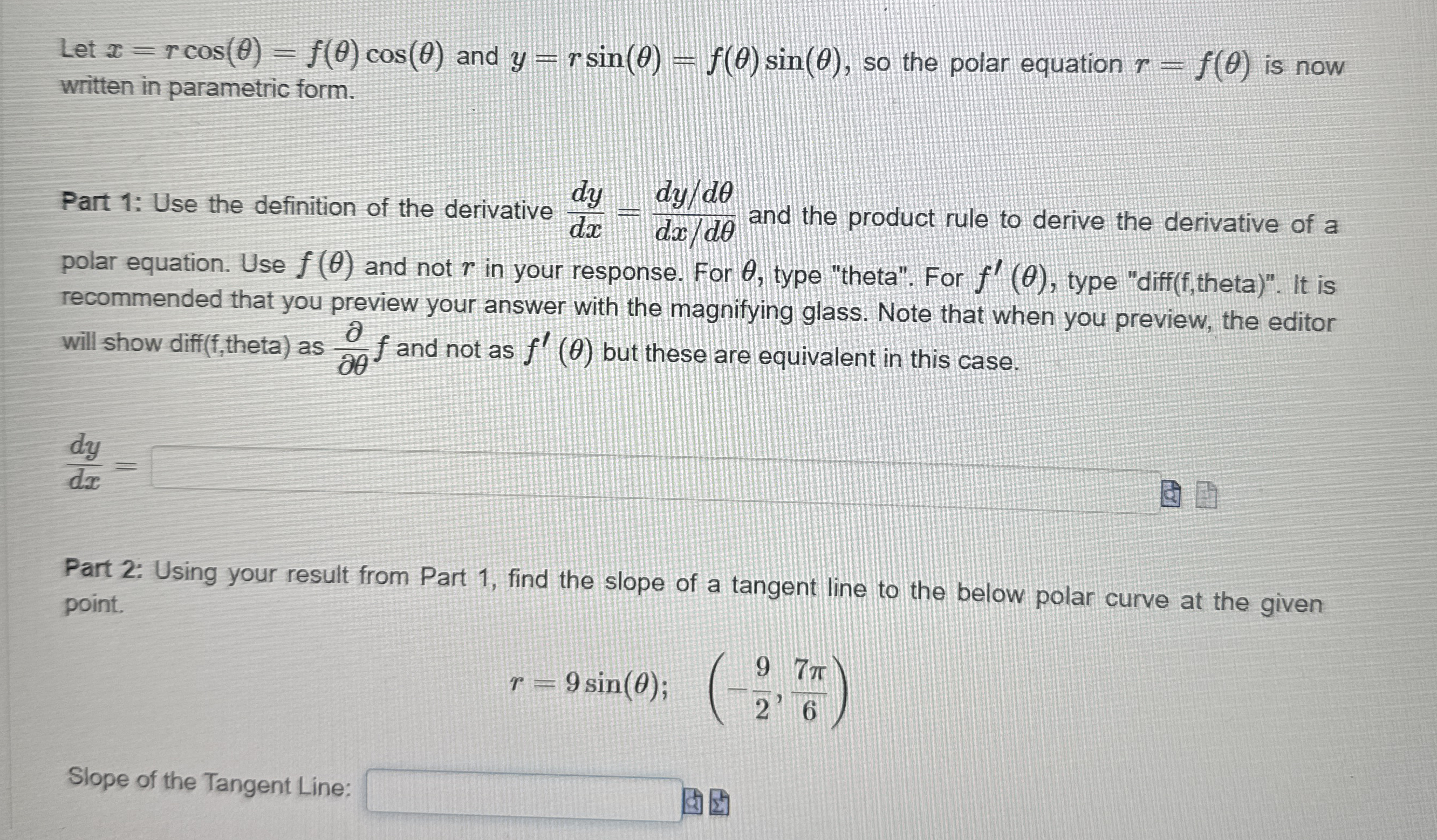
Let $x=rcos()=f()cos()$ and $y=rsin()=f()sin(),$ so the polar equation $r=f()$ is now written in parametric form.

Part $1$: Use the definition of the derivative $\frac{dy}{dx}=\frac{d\frac{y}{d}}{d\frac{x}{d}}$ and the product rule to derive the derivative of a polar equation. Use $f()$ and not $r$ in your response. For $,$ type "theta". For $f^{\text{'}}(),$ type "diff$(,$ theta$)".$ It is recommended that you preview your answer with the magnifying glass. Note that when you preview, the editor will show diff$(f,$ theta$)$ as $\frac{\text{d}\text{e}\text{l}}{\text{d}\text{e}\text{l}}f$ and not as $f^{\text{'}}()$ but these are equivalent in this case.

$\frac{dy}{dx}=$

$$

Part $2$: Using your result from Part $1,$ find the slope of a tangent line to the below polar curve at the given point.

$r=9sin()$;$,(-\frac{9}{2},\frac{7}{6})$

Slope of the Tangent Line: