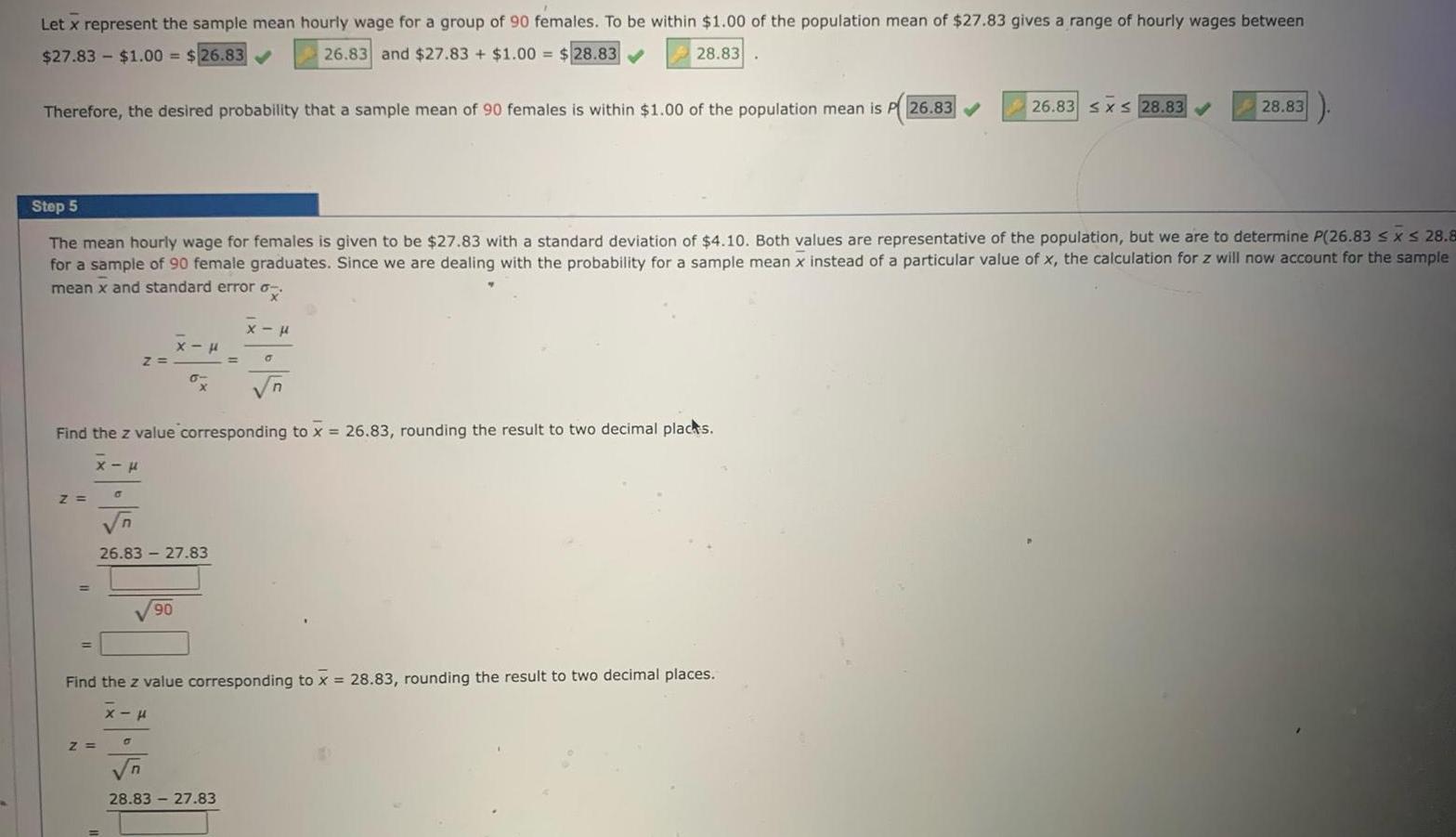
Let x represent the sample mean hourly wage for a group of 90 females. To be within $1.00 of the population mean of $27.83 gives a range of hourly wages between $27.83 $1.00 = $26.83 26.83 and $27.83 + $1.00 = $28.83 28.83 Therefore, the desired probability that a sample mean of 90 females is within $1.00 of the population mean is P 26.83 26.83 x 28.83 28.83 Step 5 The mean hourly wage for females is given to be $27.83 with a standard deviation of $4.10. Both values are representative of the population, but we are to determine P(26.83 x 28.8 for a sample of 90 female graduates. Since we are dealing with the probability for a sample mean x instead of a particular value of x, the calculation for z will now account for the sample mean x and standard error -. X-F Z= = x Find the z value corresponding to x = 26.83, rounding the result to two decimal places. Z=> n 26.83 27.83 = 90 Find the z value corresponding to x = 28.83, rounding the result to two decimal places. -x Z= n 28.83-27.83