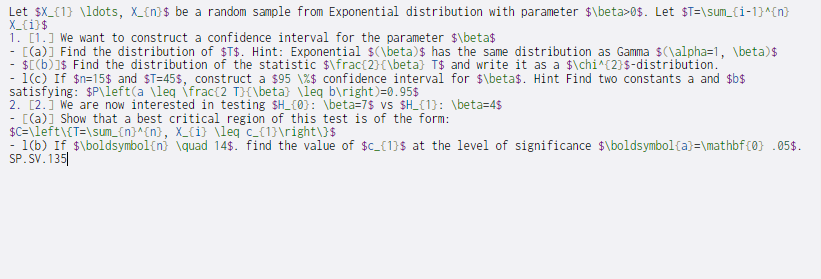
Let $X_{1} \ldots, X_{n}$ be a random sample from Exponential distribution with parameter $\beta>0$. Let $T=\sum_{i-1}^{n} X_{i}$ 1. [1.] We want to construct a confidence interval for the parameter $\beta$ - [(a)] Find the distribution of $T$. Hint: Exponential $(\beta)$ has the same distribution as Gamma $(\alpha=1, \beta) - $[(b)]$ Find the distribution of the statistic $\frac{2}{\beta) T$ and write it as a $\chi^{2}$-distribution. - 1) If $n=15$ and $T=455, construct a $95 \%$ confidence interval for $\beta$. Hint Find two constants a and $b$ satisfying: $P\left( \leq \frac{2 T}\beta} \leq b ight)=0.95$ 2. [2.We are now interested in testing SH_{0}: \beta=7$ vs $H_{1}: \beta=45 - [(a)] Show that a best critical region of this test is of the form: $C=\left\{T=\sum_{n}^{n}, X_{i} \leq c_{1} ight\}$ -1(b) If $\boldsymbol{n} \quad 14$. find the value of $c_{1}$ at the level of significance $\boldsymbol{a}=\mathbf {0} .05$. SP.SV.135