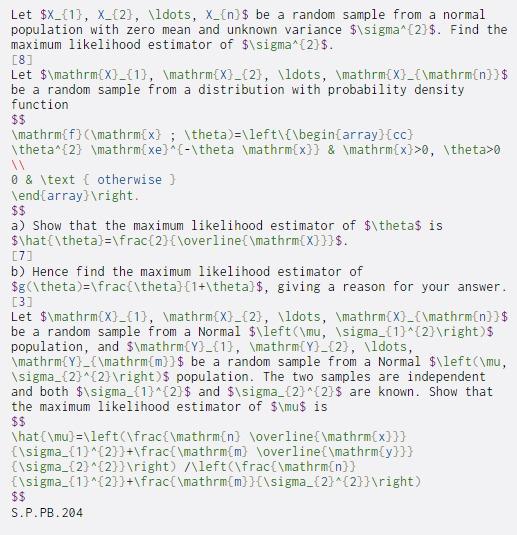
Let $X_{1}, X_{2}, \ldots, X_{n}$ be a random sample from a normal population with zero mean and unknown variance $\sigma^{2}$. Find the maximum likelihood estimator of $\sigma^{2}$. [8] Let $\mathrm{X}_{1}, \mathrm{X}_{2}, \ldots, \mathrm{X}_{\mathrm{n}}$ be a random sample from a distribution with probability density function $$ \mathrm{f}(\mathrm{x} ; \theta)=\left\{\begin{array}{cc) \theta^{2} \mathrm{xe}^{-\theta \mathrm{x}} & \mathrm{x}>0, \theta>0 0 & \text { otherwise } \end{array} ight. $$ a) Show that the maximum likelihood estimator of $\theta$ is $\hat{\theta)=\frac{2}{\overline{\mathrm{X}}}$. [71 b) Hence find the maximum likelihood estimator of $g(\theta)=\frac{\theta}{1+\theta]$, giving a reason for your answer. [3] Let $\mathrm{X}_{1}, \mathrm{X}_{2}, \ldots, \mathrm{X)_{\mathrm{n}}$ be a random sample from a Normal $\left(\mu, \sigma_{1}^{2} ight) population, and $\mathrm{Y}_{1}, \mathrm{Y}_{2}, \ldots, \mathrm{Y}_{\mathrm{m}}$ be a random sample from a Normal $\left(\mu, \sigma_{2}^{2} ight) $ population. The two samples are independent and both $\sigma_{1}^{2}$ and $\sigma_{2}^{2}$ are known. Show that the maximum likelihood estimator of $\mu$ is $$ \hat [\mu)=\left(\frac{\mathrm{n} \overline{\mathrm{x}}} {\sigma_{1}^{2}}+\frac{\mathrm{m} \overline {\mathrm{y}}} {\sigma_{2}^{2}} ight) /\left(\frac{\mathrm{n}} {\sigma_{1}^{2}}+\frac{\mathrm{m} }{\sigma_{2}^{2}} ight) $$ S.P.PB. 204