Question: Let $X_{1), X_{2), X_{3}$ be independent, identically distributed continuous random variables. Find the probability that the second largest value (i.e., the median) is closer to

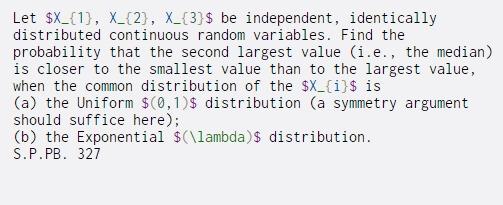
$Let $X_{1), X_{2), X_{3}$ be independent, identically distributed continuous random variables.$

Let $X_{1), X_{2), X_{3}$ be independent, identically distributed continuous random variables. Find the probability that the second largest value (i.e., the median) is closer to the smallest value than to the largest value, when the common distribution of the $X_{i}$ is (a) the Uniform $(0,1)$ distribution (a symmetry argument should suffice here); (b) the Exponential $(\lambda)$ distribution. S.P.PB. 327

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Problem 3 Let X1. .... X, be independent and identically distributed continuous random variables with a positive continuous joint probability density function f(x1. . . ., X'n). 3pts (i) Suppose that...

solve this question Problem 3 Let X1. .... X, be independent and identically distributed continuous random variables with a positive continuous joint probability density function f(x1. . . ., X'n)....

6. Let X1, X2. ..., Xn be independent and identically distributed random variables from [18 Marks] Uniform(0,1) distribution. Let X() and X(n) denote the smallest and the largest order statistics,...

CST.20assign data Extract = dataStore; endmodule (a) What would be suitable comments on the behaviour of the code at points "comment A" to "comment D"? [4 marks] (b) In the synthesised...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

You are a contestant on a television game show. Before you are three closed doors. One of them hides a car, which you want to win; the other two hide goats (which you do not want to win). First you...

AMS 311, Spring 2016 Homework 10 Due at the beginning of class, May 03, 2016 1. (20 points) Assume that X and Y are independent and identically distributed Uniform(0,1) random variables. (a) (10...

1 Let X1, X2,..., Xg, be independent and identically distributed continuous random variables, each with expected value u= E(X) = 5, and variance o- = V(X) = 4. Determine the sampling distribution of...

SUMMARY this journal, the length of it should not be more than 2 pages, with 1.5 spacing size 12 Times New Rome. Available online at www.sciencedirect.com Journal of Empirical Finance 15 (2008) 199 -...

Let X1, X2, . . . , be independent and identically dis tributed (i.i.d.) continuous random variables with common distribution FX (x) = P{Xi x}. We say that a record occurs at time n, n > 0 and has...

In August 2010, Wentao Chen, manager of Danshui Plant No. 2 in southern China, was anxious. The plant was in the third month of a 12-month contract to assemble the Apple iPhone 4. The contract called...

Compare owners equity in a sole proprietorship, partners equity in a partnership, and stockholders equity in a corporation.

Question 1 6 1 pts If its yield to maturity declined by 1 % , which of the following bonds would have the largest percentage increase in valoe? A 1 - year zero coupon bond. A T - ycar bood withan 5 %...

Seved Help 14 Wisconsin Snowmobile Corp. is considering a switch to level production Cost efficiencies would occur under level production, and aftertax costs would decline by $31,500, but inventory...

2. Explain how the role of training is changing.

7. General Mills

1. Discuss how business strategy influences the type and amount of training in a company.