Let X1,..., Xn be iid Bernoulli random variables with unknown parameter p e (0,1)

Suppose we want to test

H0: p e [0.48, 0.51]

H1: p not e [0.48,0.51]

We want to construct an asymptotic test psy for these hypotheses using Xn_bar.

For this problem, we specifically consider the faimly of test "psy_c1,c2", where we reject the null hypothesis if either:

-> Xn_bar

-> Xn_bar >c2 >= 0.51 for some c1 and c2 that may depend on n, ie

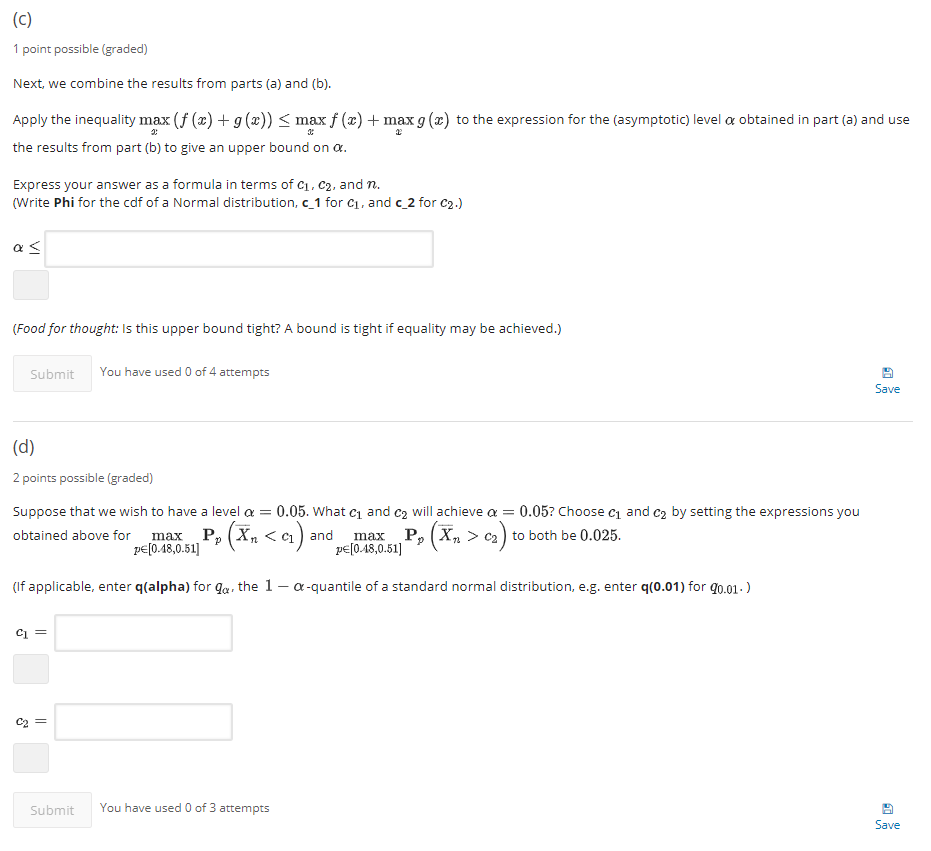
"psy_c1,c2"= 1((Xn_bar c2)), where c1

( C ) 1 point possible ( graded ) Next , we combine the results from parts laj and ( b ) . Apply the inequality max ( f ( * ) + g ( a ) ) = max f ( * ) + max g (`` ) to the Expression for the (asymptotic level * obtained in part (a ) and LEE the results from part ibj to give an upper bound on * . Express your answer as a formula in terms of . CZ . and M.\\ I Write Phi for the calf of a Normal distribution , c_ 1 for (1 , and c_ 2 for cz . ) I Food for thought : Is this upper bound tight ? A bound is tight if Equality may be achieved . ! Submit\\ "You have USEd O of 4 attempts* SAVE ( d) 2 points possible [graded! SUPPOSE that WE wish to have a level * = 0.05 . What `1 and oz will achieve * = 0.05 ? Choose ", and oz by setting the Expressions you* obtained above for max P ( In C2) for large n. Express your answers as a formula in terms of c1, C2, n and p. (Write Phi for the cdf of a Normal distribution, c_1 for ci, and c_2 for c2.) P, (X, C2 )~ For what value of p E [0.48, 0.51] is the expression above for Pp (Xn > cz) maximized? P, (Xn. > C2 ) is max at p = Submit You have used 0 of 4 attempts Save