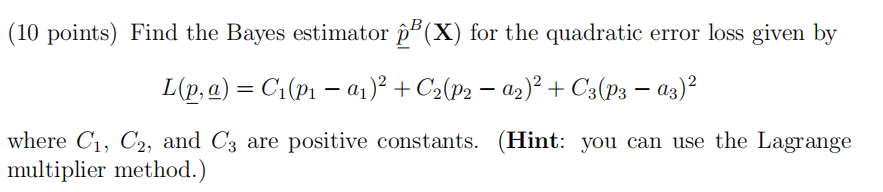
Let Xi, i = 1,..., N be a random sample where the X; take only three possible values x1, x2 and x3 with probability P1, P2 and P3 respectively. Here p + p2 + P3 = 1 and p = (P1, P2, P3) is the vector of unknown parameters. Thus the p.m.f. of the X; is p(x|p)= = Pk x = xk, k = 1,2,3 otherwise 0 For notational simplicity, we will assume that x = 1, x2 = 2, x3 = 3 but the discussion below is general. (10 points) Show that the g(p; a) form a conjugate family of prior distribution for the sample X. Assuming that the hyperparamter for the prior distribution are a, find the hyperparamter a' for the posterior distribution. (10 points) Find the Bayes estimator (X) for the quadratic error loss given by L(p, a) = C(p1 a) + C2 (P2 a2) + C3 (P3 3) - - - where C1, C2, and C3 are positive constants. (Hint: you can use the Lagrange multiplier method.)