Question: . Let (Xn, n = 0, 1, 2,...) and (Yn, n = 0, 1, 2,...) be two symmetric random walks in Z, such that
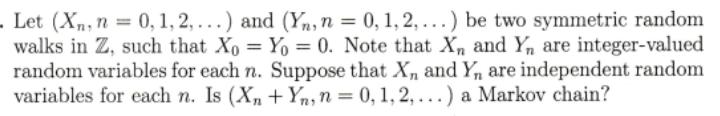
. Let (Xn, n = 0, 1, 2,...) and (Yn, n = 0, 1, 2,...) be two symmetric random walks in Z, such that Xo Yo = 0. Note that X and Yn are integer-valued random variables for each n. Suppose that X and Yn are independent random variables for each n. Is (Xn+Yn, n = 0, 1, 2,...) a Markov chain? . Let (Xn, n = 0, 1, 2,...) and (Yn, n = 0, 1, 2,...) be two symmetric random walks in Z, such that Xo Yo = 0. Note that X and Yn are integer-valued random variables for each n. Suppose that X and Yn are independent random variables for each n. Is (Xn+Yn, n = 0, 1, 2,...) a Markov chain?
Step by Step Solution
3.40 Rating (153 Votes )
There are 3 Steps involved in it
Two random walks are said to be independent if the probability of any sequence of steps of one walk is independent of the sequence of steps of the oth... View full answer

Get step-by-step solutions from verified subject matter experts


