Question: Let {Y, Y2,..., Yn} be an identically distributed sample selected from a population via simple random sampling without replacement (SRSWOR), where E[Y;] = and
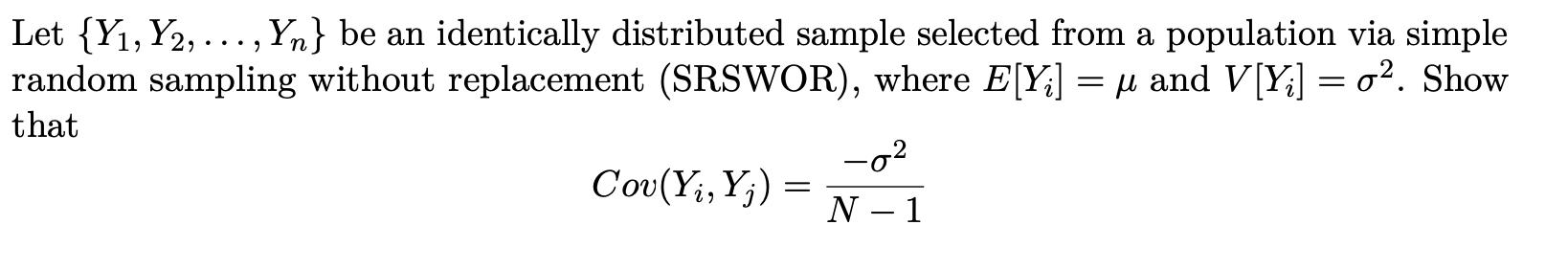
![Hint: \( \operatorname{Cov}\left(Y_{i}, Y_{j}ight)=E\left[\left(Y_{i}-\muight)\left(Y_{j}-\muight)ight]=E\left[Y_{i}](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2023/03/641e9396c8a62_1679725458401.jpg)
Let {Y, Y2,..., Yn} be an identically distributed sample selected from a population via simple random sampling without replacement (SRSWOR), where E[Y;] = and V[Y] = o. Show that Cov(Yi, Yj) = -0 N - 1 Hint: Cov(Y, Yj) = E[(Y )(Yj )] = E[Y;Y] . Let U, U2, ..., UN be the values from the population. First, show that 2 N N 1 Cov(Yi, Y) = [U; ( ) U - v ( + ) ( ) - (u.) . Uj (v1) U N N i#j N 1 U Uj 1 2 - + [2 (5-4-) - + (20) ] [Ui N N 1 N Now, show how you can get from above to: Cov(Yi, Yj) = 2 N N (8) - $ * - + (2x)]) | Ui U? N 2 Ui N N - 1 i=1
Step by Step Solution
3.33 Rating (150 Votes )
There are 3 Steps involved in it
To show that CovYi Y 2N1 we can follow these steps 1 Start with the given equation CovYi Y EYi Y 2 E... View full answer

Get step-by-step solutions from verified subject matter experts


