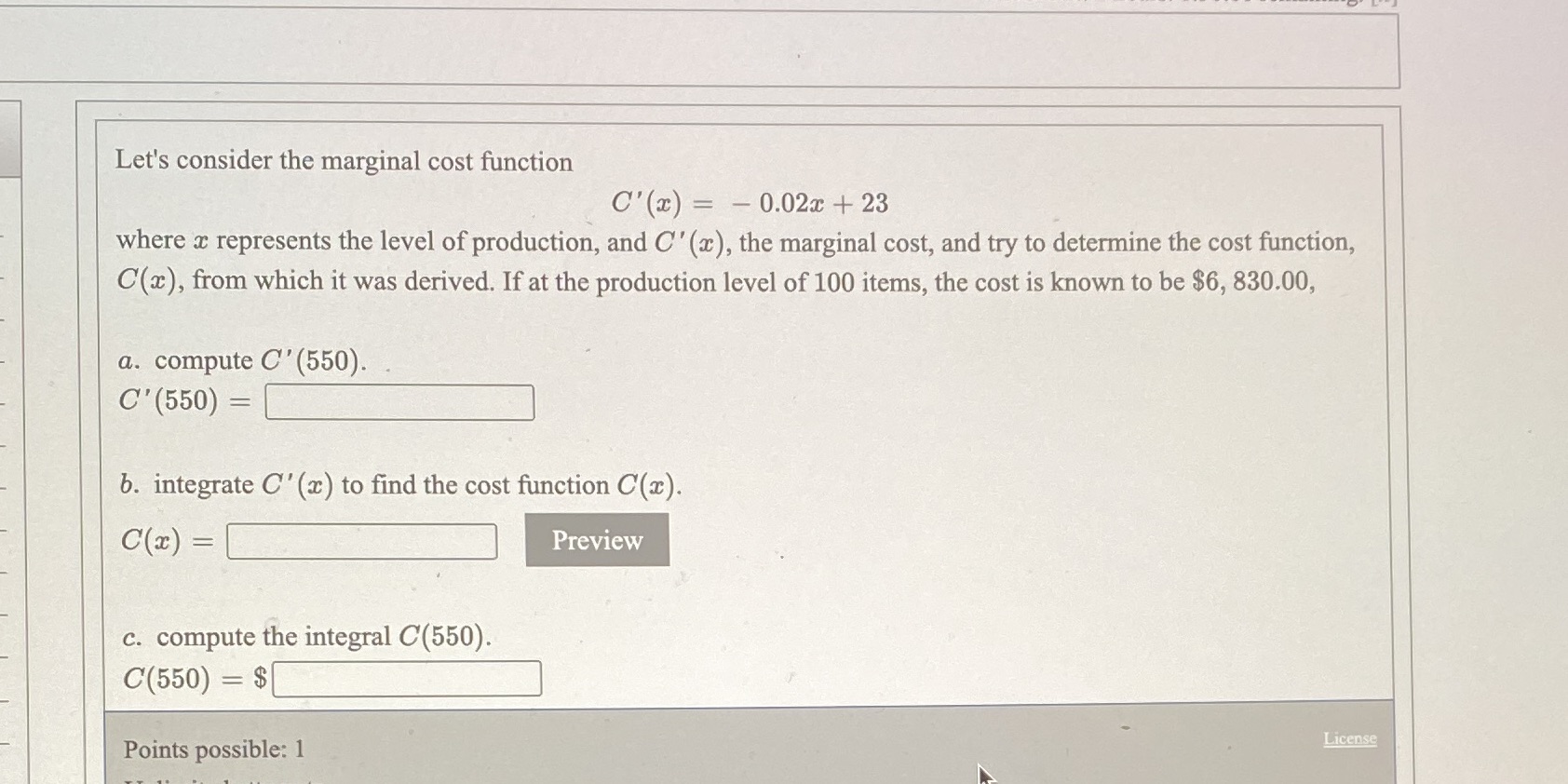
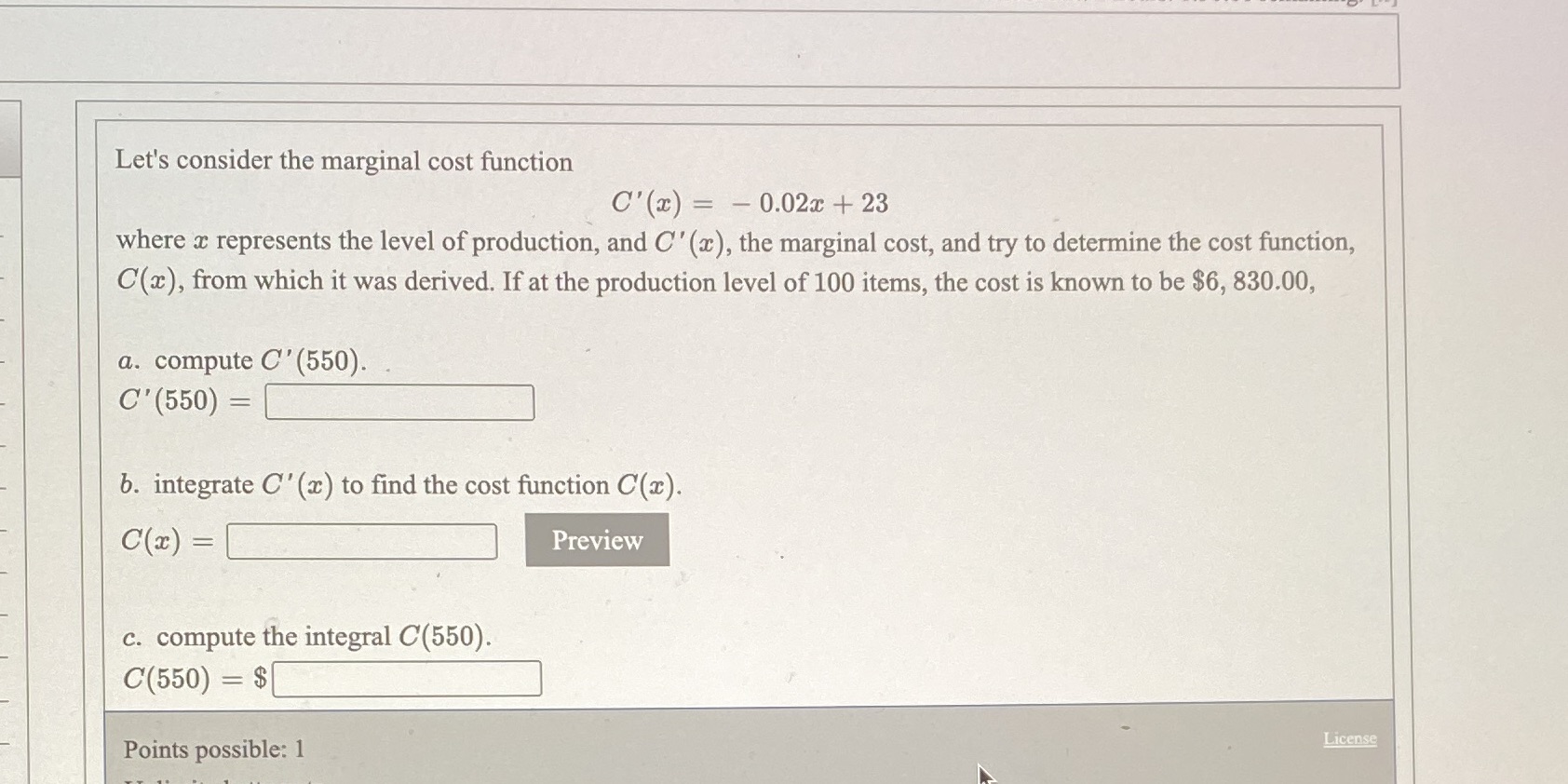
Let's consider the marginal cost function C'(2) = - 0.02x + 23 where x represents the level of production, and C' (x), the marginal cost, and try to determine the cost function, C(a), from which it was derived. If at the production level of 100 items, the cost is known to be $6, 830.00, a. compute C' (550). C' (550) = b. integrate C' (x) to find the cost function C(x). C(x) = Preview c. compute the integral C(550). C(550) = $ Points possible: 1 License