Question: Let's prove that for all c, In (cosh(x)) > - In(2) For all c ec Number By adding to both sides of this inequality Since

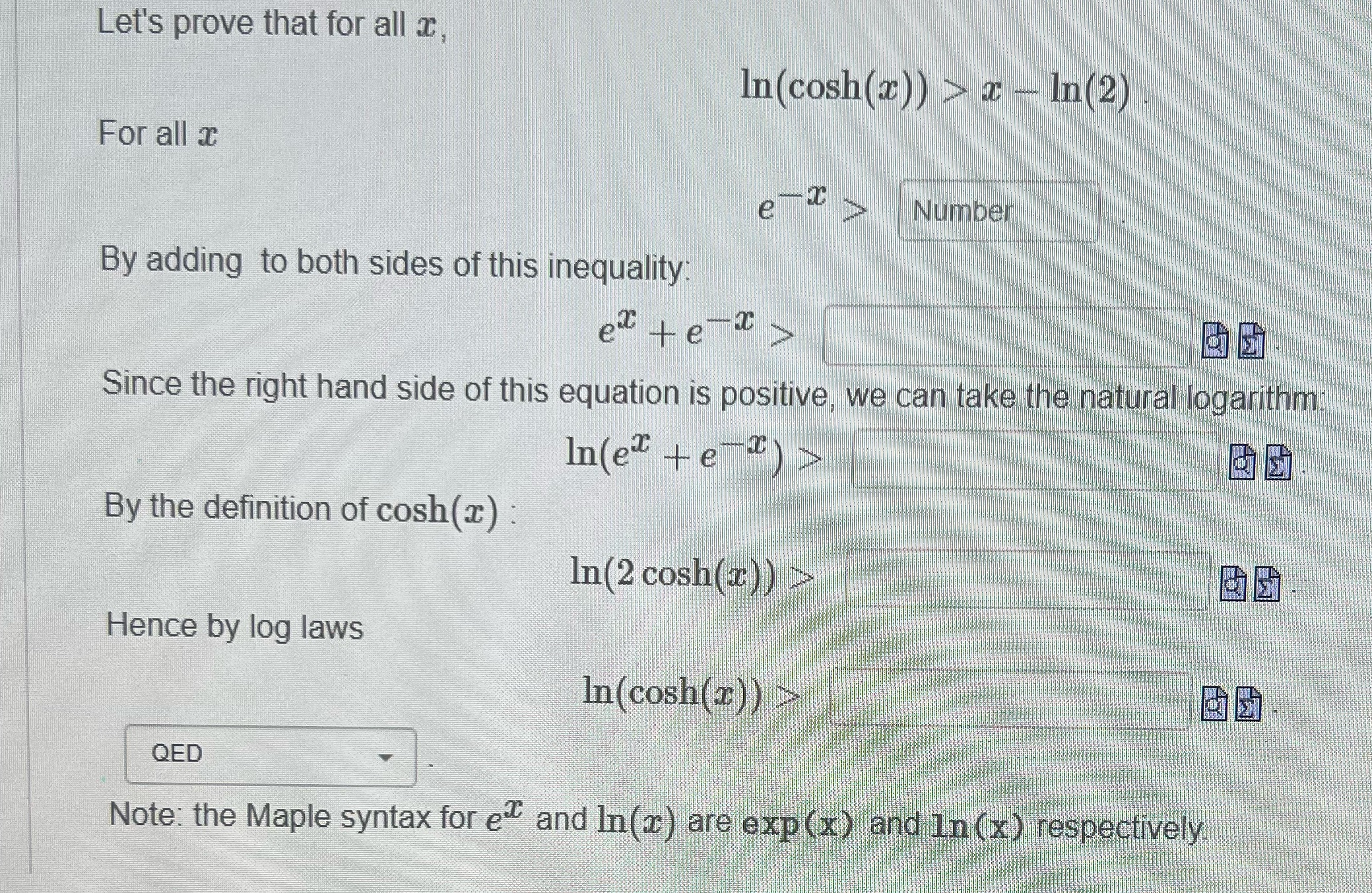
Let's prove that for all c, In (cosh(x)) > - In(2) For all c ec Number By adding to both sides of this inequality Since the right hand side of this equation is positive, we can take the natural logarithm; In(e te " ) > By the definition of cosh (a) : In(2 cosh(I)) Hence by log laws In (cosh(z)) = QED Note: the Maple syntax for ed and In(a) are exp (x) and In (x) respectively

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Describing Data Once we have collected data from surveys or experiments, we need to summarize and present the data in a way that will be meaningful to the reader. We will begin with graphical...

MAT 275 Laboratory 7 Laplace Transform and the Symbolic Math Toolbox In this laboratory session we will learn how to 1. Use the Symbolic Math Toolbox 2. Calculate the Laplace and Inverse Laplace...

Here is the new homework question. Please review the General Homework instructions due to the instructor being so strict. Were there any podcasts or Homework document notes that you needed me to...

answer this question as soon as possible. the worksheet 8 is given below all the last three files are given below. the first file is 1000 prime text it contain text 1 from 7919 numbers. second file...

87 Chapter 7 Sequencing MIDI Overview I n this chapter we will examine advanced MIDI sequencing concepts using Ableton Live, a powerful digital audio workstation. This chapter will also serve as a...

CAN U PLEASE HELP ME ANSWER THE QUESTIONAIRE BELOW BASED ON THE PICS THAT I WILL ATTACH . The Negotiation Checklist (Abbreviated from Simons & Tripp, 1997) About You What is your overall goal? What...

A/B Testing HW Article Link Here: https://www.dropbox.com/s/jqq1xq1f9nf7354/HW3_recycling.pdf?dl=0 Problem 1 - Interpreting Regression Results: Recycling [26 points] Entrepreneurs introducing new...

Instructions: Your first task will be to determine how many people have applied for which areas of study thus far. To do this: Open the file Highlight the column "Desired Area of Study" Select...

Show work/explanation where indicated. Answers without any work may earn little, if any, credit. You may type or write your work in your copy of the exam, or if you prefer, create a document...

Formulate the following questions. 2 2 2 2 ,3 ,2,,,[] {i} _,, ,2_2,,,[] {2] =4: C 2:? 2!? A 2A 2A Factoring our binomials we get: E 2 E 2 D 2 or2 A = F C[y+2r:] 4c [x 2,4] combining like terms gives:...

a) Determine the poles and zeros of the system and show them on the complex plane. (Hint: You may use roots() and pzmap() command of MATLAB.) b) Considering the locations of the poles, comment on the...

For the r x r Latin square design, show that (r - 1)o? + rEr. E(SSTr)

9. Using the value of K in Problem 8, compute the gain and phase margins when T d = 0.2. a. G M . . = 14 dB, P M . . = 27 b. G M . . = 20 dB, P M . . = 64.9 c. G M . . = dB, P M . . = 60 d....

In Chapter 3, the consumption and creation of several types of energy were described; solar, kinetic, tidal, volcanic, earthquake, thermal, combustion, electrical, potential, wind. Describe two...

A bar of mild steel is stressed to the point where general yielding occurs and the test is interrupted prior to necking. Draw the stress-strain curve and describe the stress-strain response...

BOGO Company segments its company into four distinct divisions. The net revenues, operating profit, and total assets for these divisions are disclosed in the footnotes to BOGO Company's consolidated...

When Sue returned from her meeting with the CFO, there was a note from the Wine bottle facility manager, Ron Cross, waiting for her at her desk. She read through the note with enthusiasm, noting in...

REVIEW THE INFORMATION ABOUT LEAPFROG HOSPITAL SAFETY GRADES. CHOOSE TWO HOSPITALS TO COMPARE A VERY EFFECTIVE ONE AND ONE WHICH IS NOT EFFECTIVE. WHAT SEPARATES THE TWO? HOW CAN THE A HOSPITAL USE...

1. To gain insight into why we believe more in one type of information than another.

2. In this chapter, the reader should reflect on the following concepts: emo-tional information, concrete information, local information, the reference object, consensus information, conflict...

11. Give two examples of each of the following heuristic assessment mechanisms. a) We use the information that is currently accessible. b) We assume an initial anchor point (value). c) We compare to...