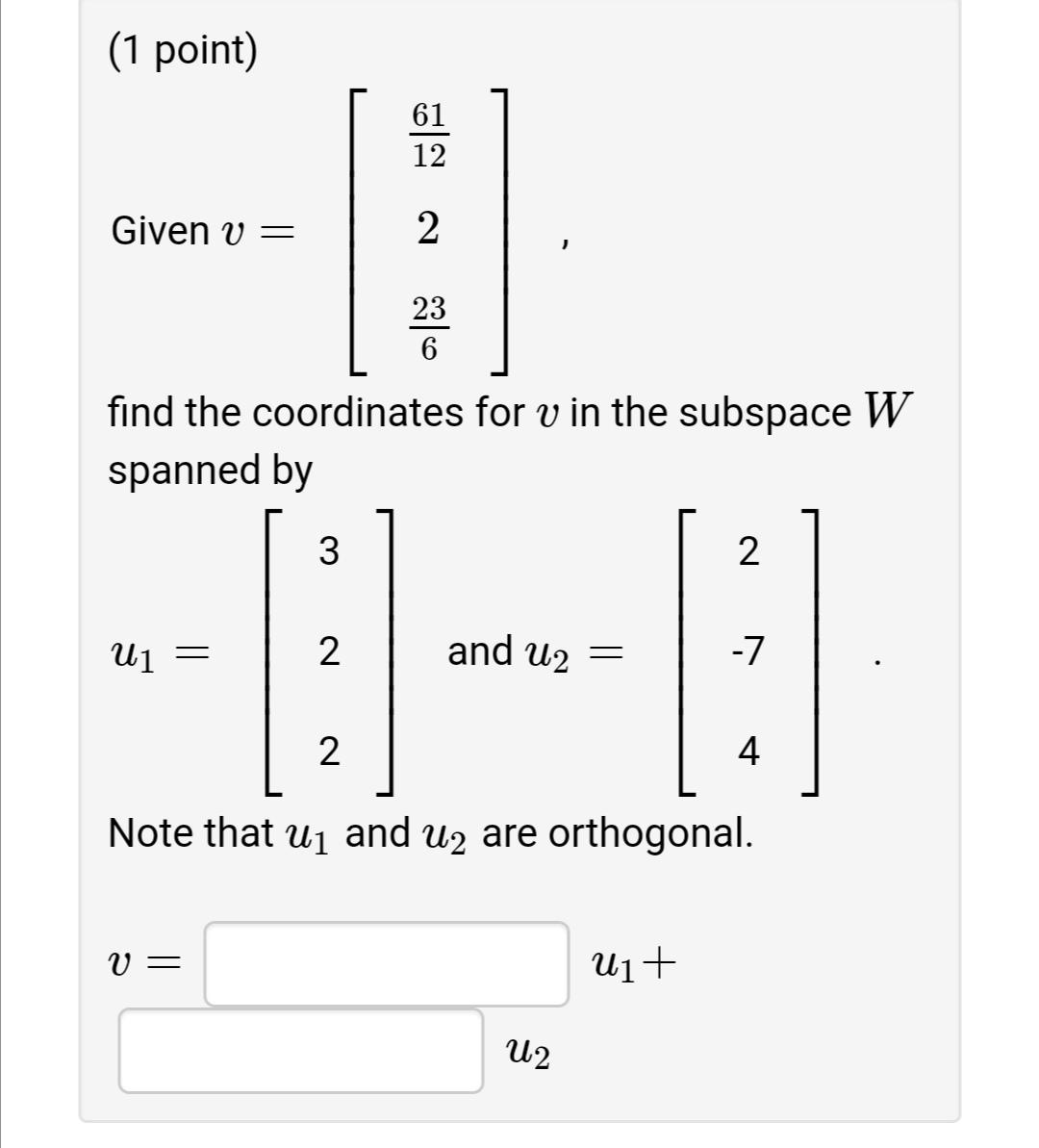
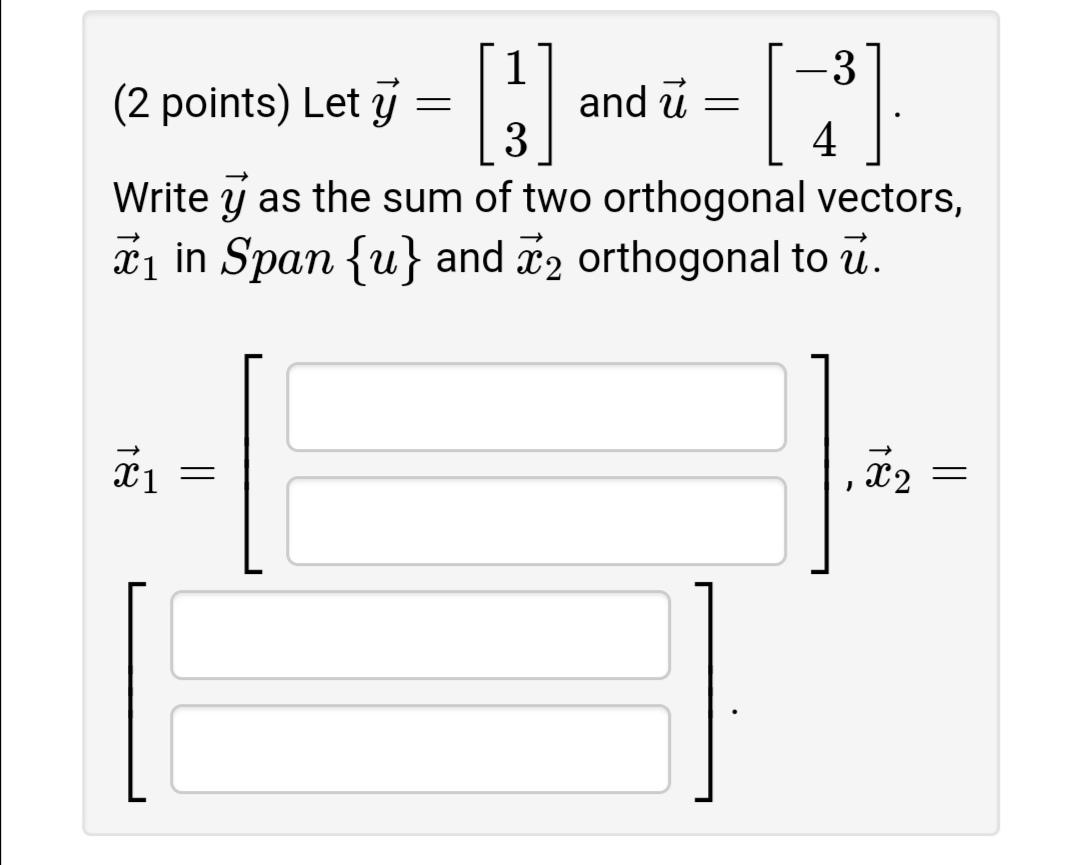
All vectors and subspaces are in R". Check the true statements below: A. For each y and each subspace W, the vector y projw(y) is orthogonal to W. B. If z is orthogonal to u1 and u2 and if W = Span{u1, u2}, then z must be in W+. C. If y is in a subspace W, then the orthogonal projection of y onto W is y itself. - OD. The orthogonal projection of y onto a subspace W can sometimes depend on the orthogonal basis for W used to compute . E. If the columns of an n x p matrix U are orthonormal, then UUTY is the orthogonal projection of y onto the column (1 point) 61 12 Given v = 2 23 6 find the coordinates for v in the subspace W spanned by 2 Uj = 2 and u2 = -7 4 Note that u1 and u2 are orthogonal. U1+ U2 1 and u 3 (2 points) Let j 4 Write y as the sum of two orthogonal vectors, ai in Span {u} and 72 orthogonal to u. X2 = (1 point) Suppose v1, V2, V3 s an orthogonal set of vectors in R. Let w be a vector in Span(v1, v2, V3) such that 26, v2 V2 -78, w v2 = V V 14, v3 V3 = 4, w V1 28, w v3 = = 8, 6. then w = V1+ V2+ V3