Linear Algebra

Final answer only - No Explanation

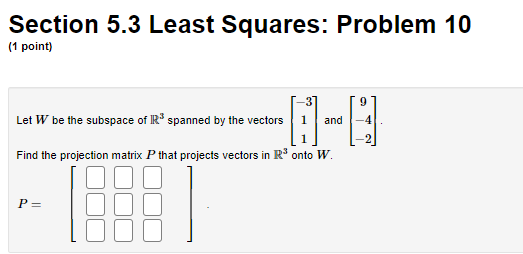
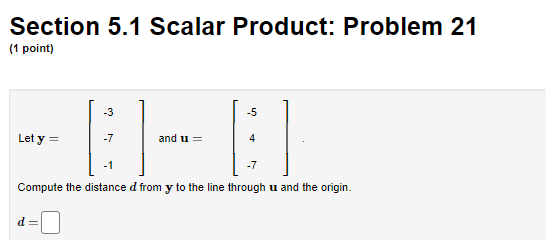
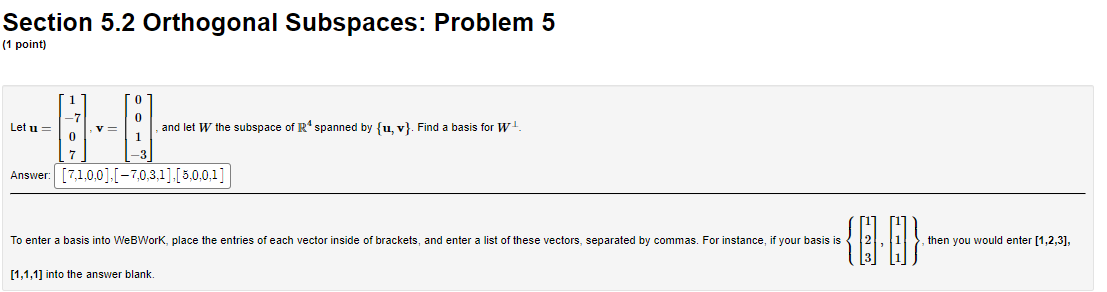
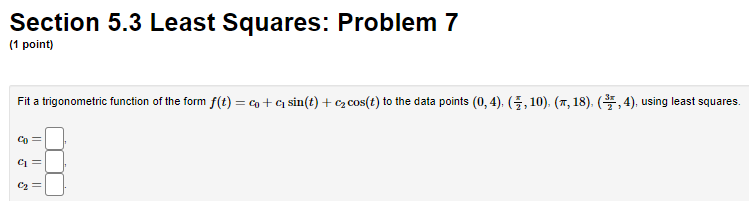
Section 5.3 Least Squares: Problem 1 (1 point) (a) Find the least-squares solution * of the system * = 181 (b) Determine the orthogonal projection p = Ax. P = Calculate the residual r(x) = b - Ax r()) =Section 5.3 Least Squares: Problem 10 (1 point) Let W be the subspace of IR spanned by the vectors Find the projection matrix P that projects vectors in R* onto W. P =Section 5.3 Least Squares: Problem 11 (1 point) The table below lists the height h (in cm), the age a (in years), the gender g (1="Male", 0="Female"), and the weight w (in kg) of some college students. Height Age Gender Weight 184 20 H 83 171 20 68 155 21 48 164 20 0 57 166 19 0 59 We wish to fit a linear function of the form f (t) = co + ch + cza + cag to these data. Find the best approximation of this form, using least squares. CoSection 5.3 Least Squares: Problem 2 (1 point) (a) Find the least-squares solution * of the system -9 X = 13 21 * = (b) Determine the orthogonal projection p = Ax P = Calculate the residual r(x) = b - Ax r(x) =Section 5.1 Scalar Product: Problem 21 (1 point) -5 Let y = -7 and 11 = 4 Compute the distance d from y to the line through u and the origin. d=Section 5.2 Orthogonal Subspaces: Problem 3 (1 point) Let L be the line spanned by 5 in IR'S. Find a basis of the orthogonal complement _ of L. Answer: [5,1.0],[-8,0,1] To enter a basis into WeBWork, place the entries of each vector inside of brackets, and enter a list of these vectors, separated by commas. For instance, if your basis is then you would enter [1,2,3], [1,1,1] into the answer blank.Section 5.2 Orthogonal Subspaces: Problem 5 (1 point) Let u = and let W the subspace of R spanned by {u, v}. Find a basis for W L. Answer: [7,1,0,0],[-7,0,3,1],[ 5,0,0,1 ] To enter a basis into WeBWork, place the entries of each vector inside of brackets, and enter a list of these vectors, separated by commas. For instance, if your basis is then you would enter [1,2,3], [1,1,1] into the answer blank.Section 5.3 Least Squares: Problem 3 (1 point) Find the least-squares solution * of the system 6 27 -5 X= -18 -4 * = 0 1Section 5.3 Least Squares: Problem 4 (1 point) Find the least-squares solution * of the system -1 -17 09 1 1 1 K= 1 1 -1 1 * =Section 5.3 Least Squares: Problem 5 (1 point) Fit a linear function of the form f(t) = c + cit to the data points (-7, -23), (0, -5), (7, 19), using least squares.Section 5.3 Least Squares: Problem 6 (1 point) Fit a quadratic function of the form f(t) = co + cit + cat to the data points (0, 4), (1, -4), (2, 4), (3, -12), using least squares. CI=Section 5.3 Least Squares: Problem 7 (1 point) Fit a trigonometric function of the form f(t) = co + a sin(t) + c2 cos(#) to the data points (0, 4), (=, 10), (#, 18), (-, 4), using least squares CISection 5.3 Least Squares: Problem 8 (1 point) -117 CT Find the orthogonal projection of v = 12 onto the subspace V of R spanned by -4 and 10 projv (v) =Section 5.3 Least Squares: Problem 9 (1 point) [19 Find the orthogonal projection of v = 6 onto the plane -I1 + 12 + 313 = 0 projection =