Linear model

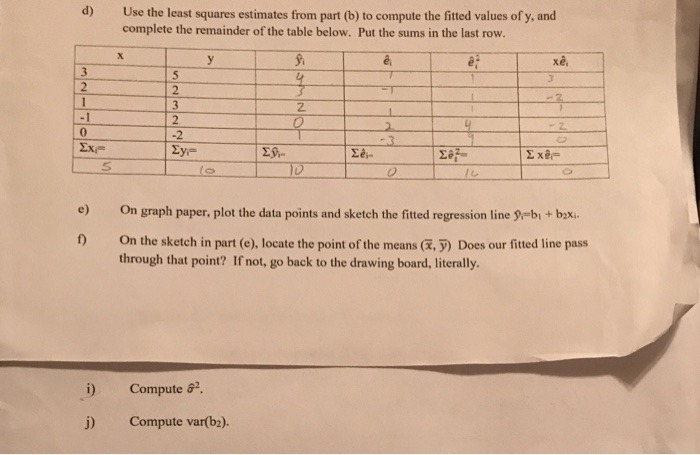
Consider the linear model Y = alX1 + a2X2 +b where the vector ( X1, X2) has a bivariate Gaussian distribution with means #1, #2, variances of, 02, and correlation coefficient p12. Consider the vector (X1, Y). One can show (via some involved calculus) that (X1, Y) has a bivariate Gaussian distribution. Determine its two means, two variances, covariance, and correlation coefficient. Remark: In lecture we considered precisely this problem but under the as- sumption that X] and X2 are independent.\fd) Use the least squares estimates from part (b) to compute the fitted values of y, and complete the remainder of the table below. Put the sums in the last row. X y e; xe J NOW W N U -Z Z 2 2 - Z 0 -2 - 3 I xef 5 TO e ) On graph paper, plot the data points and sketch the fitted regression line 9,=bj + baxi. On the sketch in part (e), locate the point of the means (x, y) Does our fitted line pass through that point? If not, go back to the drawing board, literally. i) Compute &. j) Compute var(b2).Let g (t) be the rectangular pulse shown below. The random process X (t) is defined as X(t) = Ag(t), where A is uniformly distributed between -1 and +1. 0 (1, if 0