Linear Programming for finding Nash Equilibrium in Zero-Sum Games (Rock, Paper, Scissors)

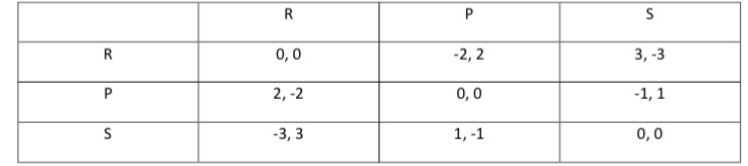
Part I. Consider the Rock, Paper, Scissors Game and find the Nash equilibrium linear program approach to write AMPL code.

• For Part I and Part II each , The Linear Program #1 to find the mixed strategy x* for player #2, The Linear Program #2 to find the mixed strategy y* for player #1, Report the expected payoffs received by the players in the Nash equilibrium found

0.0 -2.2 3. 3 2. 2 0.0 -1.1 -3.3 1, -1 0.0 1. Describe the linear program (in terms of AMPL code) in terms of payoffs of Player #2 to find the security strategy x* (i.e.) for Player #2. What is the mixed strategy x* you got when you solve the linear program? What is the optimal solution value i.e. the max min value received by Player #2)? 2. Describe the linear program (in terms of AMPL code) in terms of payoffs of the Player #2 to find the security strategy y* (i.e.) for Player #1. What is the mixed strategy y* you got when you solve the linear program? What is the optimal solution value (i.e. the min max value received by Player #2)? 3. When player #1 adopts y* and player #2 adopts x* as their strategies, what is the expected payoff for Player #1 and what is the expected payoff for Player #2 respectively?. Part II. Do the same things as described in Part I above to find a Nash equilibrium (x*, y*) for the zero-sum game below. 112 M R -1, 1 4,-4 7,-7 2, -2 -3, 3 -9,9 0.0 -2.2 3. 3 2. 2 0.0 -1.1 -3.3 1, -1 0.0 1. Describe the linear program (in terms of AMPL code) in terms of payoffs of Player #2 to find the security strategy x* (i.e.) for Player #2. What is the mixed strategy x* you got when you solve the linear program? What is the optimal solution value i.e. the max min value received by Player #2)? 2. Describe the linear program (in terms of AMPL code) in terms of payoffs of the Player #2 to find the security strategy y* (i.e.) for Player #1. What is the mixed strategy y* you got when you solve the linear program? What is the optimal solution value (i.e. the min max value received by Player #2)? 3. When player #1 adopts y* and player #2 adopts x* as their strategies, what is the expected payoff for Player #1 and what is the expected payoff for Player #2 respectively?. Part II. Do the same things as described in Part I above to find a Nash equilibrium (x*, y*) for the zero-sum game below. 112 M R -1, 1 4,-4 7,-7 2, -2 -3, 3 -9,9