linear programming

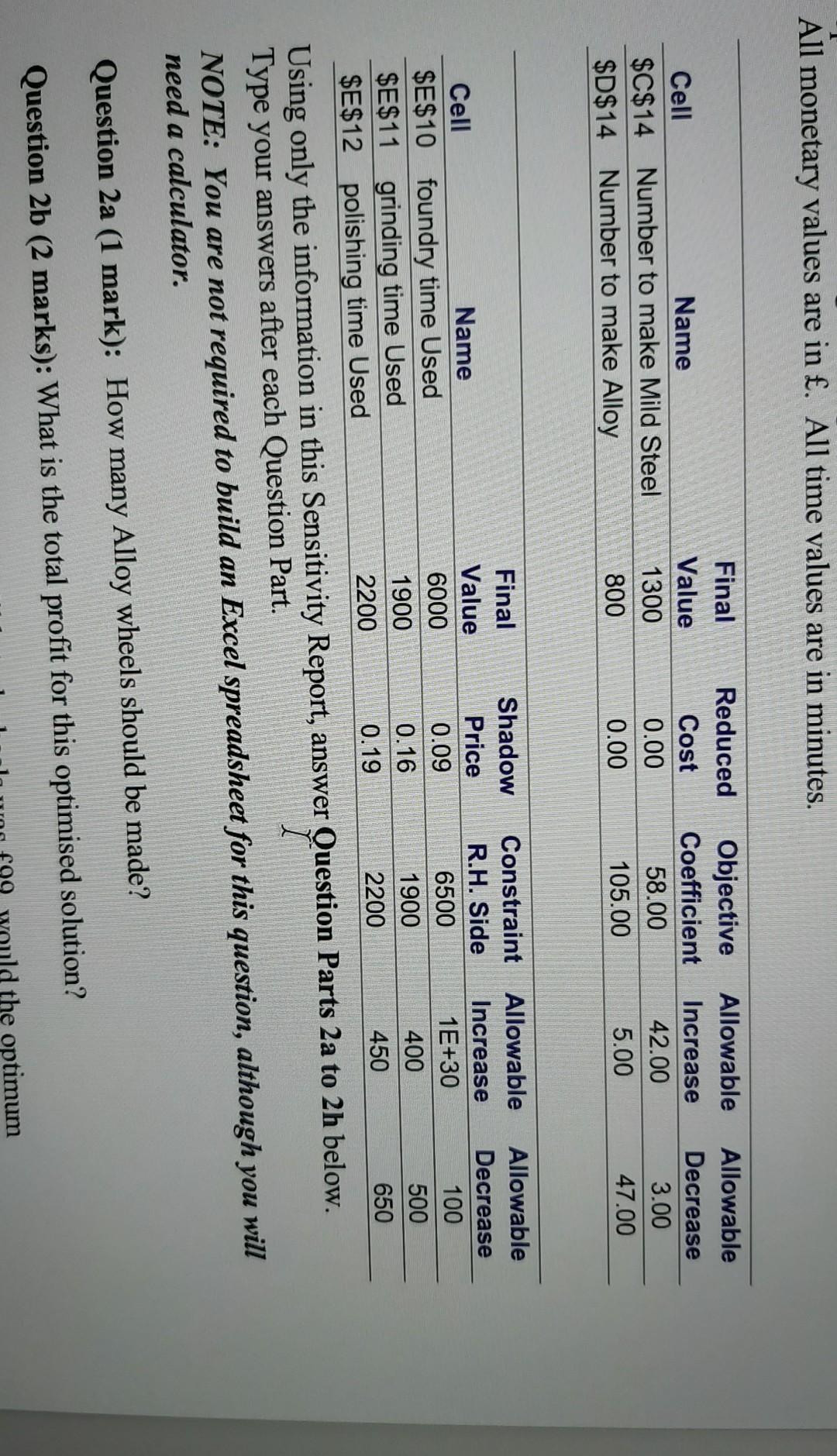
Question 2c (2 marks): If the profit on Mild steel wheels was 99, would the optimum production plan need to change? Explain why? Question 2d (1 mark): What is the lowest value to which the profit on Mild steel wheels can fall without changing the production plan, to the nearest ? Question 2e (1 mark): Which, if any, of the resources are scarce? Question 2f (1 mark): What is the maximum price which should be paid for an extra minute of polishing time, to the nearest penny? Question 2g (1 mark): What is the maximum amount of polishing time which should be bought at this price, to the nearest whole number? I Question 2h (1 mark): Should 30 more minutes of foundry time be bought at a price of 0.07 per minute? Explain why. All monetary values are in . All time values are in minutes. Cell Name $C$14 Number to make Mild Steel $D$14 Number to make Alloy Final Value 1300 800 Reduced Cost 0.00 0.00 Objective Coefficient 58.00 105.00 Allowable Increase 42.00 5.00 Allowable Decrease 3.00 47.00 Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease 6000 $E$10 foundry time Used 0.09 6500 100 1E+30 1900 1900 0.16 400 $E$11 grinding time Used 500 2200 0.19 $E$12 polishing time Used 450 2200 650 Using only the information in this Sensitivity Report, answer Question Parts 2a to 2h below. I Type your answers after each Question Part. NOTE: You are not required to build an Excel spreadsheet for this question, although you will need a calculator. Question 2a (1 mark): How many Alloy wheels should be made? Question 2b (2 marks): What is the total profit for this optimised solution? the optimum