Linear Programming

The Whole Food Nutrition Centre uses three bulk grains, A, B, and C, to blend a natural cereal that it sells by the pound. The cost of each bulk grain is indicated in the table below, along with the units of four types of nutrient (Nutrient 1, 2, 3, and 4) that is contained in each pound of the grains.

After consulting with the nutritionist, Whole Food has determined that each pound serving of the cereal should contain 24 units of Nutrient 1, 16 units of Nutrient 2, 8 units of Nutrient 3, and 3.4 units of Nutrient 4. Whole Food wishes to decide how to blend the three types of grain in order to minimize the total cost of each pound of the cereal. In other words, they wish to solve the following optimization:

Minimize 33A + 47B + 38C Subject to:

22A + 28B + 21C ? 24

16A + 14B + 25C ? 16

8A+7B +9C?8 5A + 6C ? 3.4

A+B +C=1

A,B,C > 0

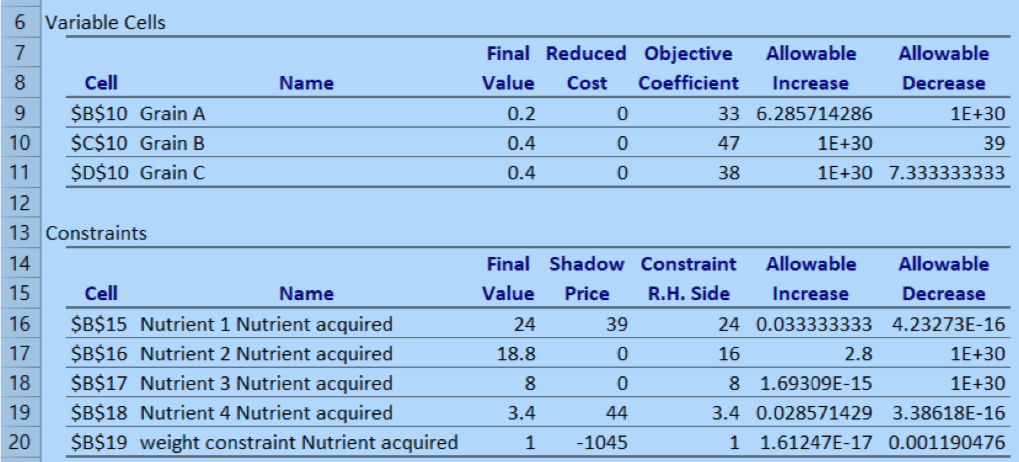
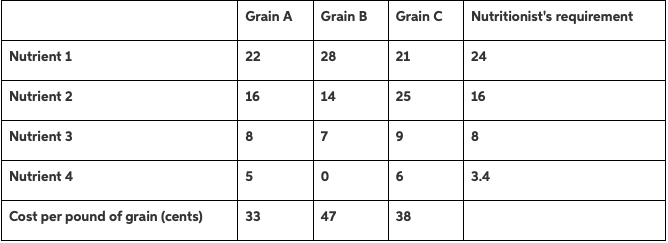
6 Variable Cells 7 Final Reduced Objective Allowable Allowable 8 Cell Name Value Cost Coefficient Increase Decrease 9 $B$10 Grain A 0.2 0 33 6.285714286 1E+30 10 $C$10 Grain B 0.4 0 47 1E+30 39 11 $D$10 Grain C 0.4 0 38 1E+30 7.333333333 12 13 Constraints 14 Final Shadow Constraint Allowable Allowable 15 Cell Name Value Price R.H. Side Increase Decrease 16 $B$15 Nutrient 1 Nutrient acquired 24 39 24 0.033333333 4.23273E-16 17 $B$16 Nutrient 2 Nutrient acquired 18.8 0 16 2.8 1E+30 18 $B$17 Nutrient 3 Nutrient acquired 8 0 8 1.69309E-15 1E+30 19 $B$18 Nutrient 4 Nutrient acquired 3.4 44 3.4 0.028571429 3.38618E-16 20 $B$19 weight constraint Nutrient acquired 1 -1045 1 1.61247E-17 0.001190476Grain A Grain B Grain C Nutritionist's requirement Nutrient 1 22 28 21 24 Nutrient 2 16 14 25 16 Nutrient 3 8 7 9 8 Nutrient 4 5 0 6 3.4 Cost per pound of grain (cents) 33 47 38