Lingo code for the following problem using sets.

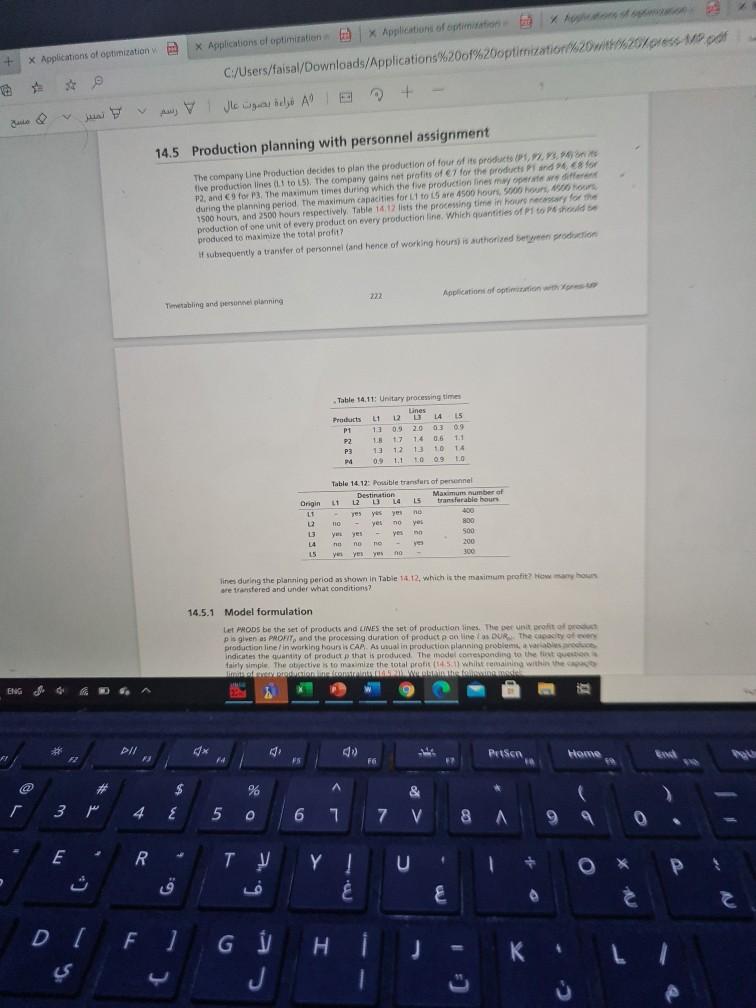
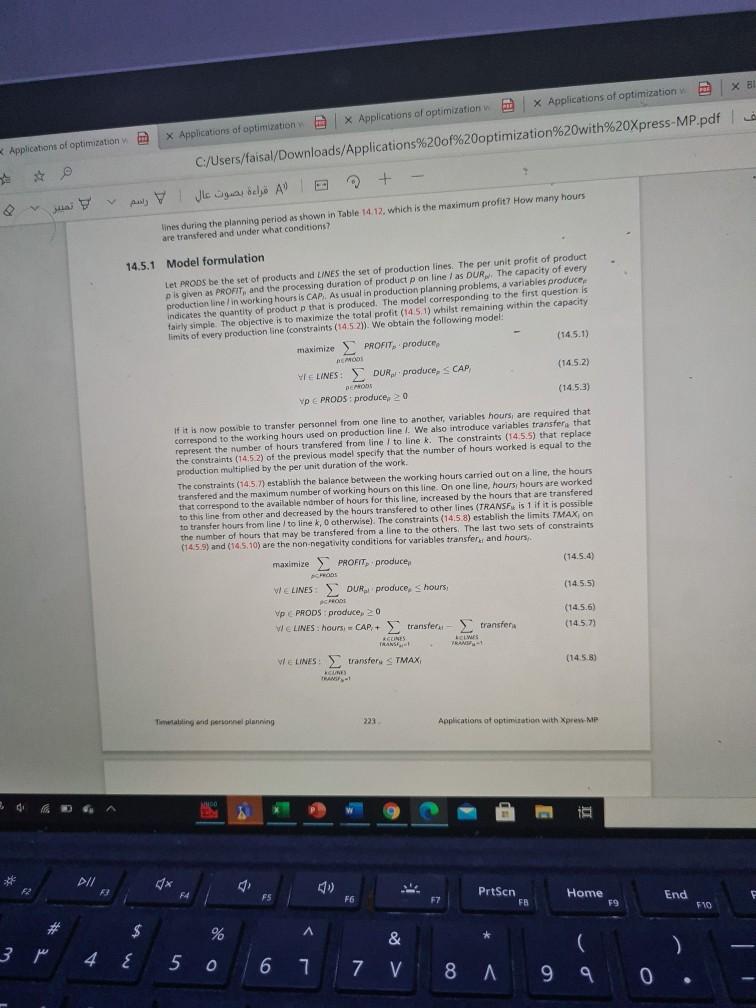
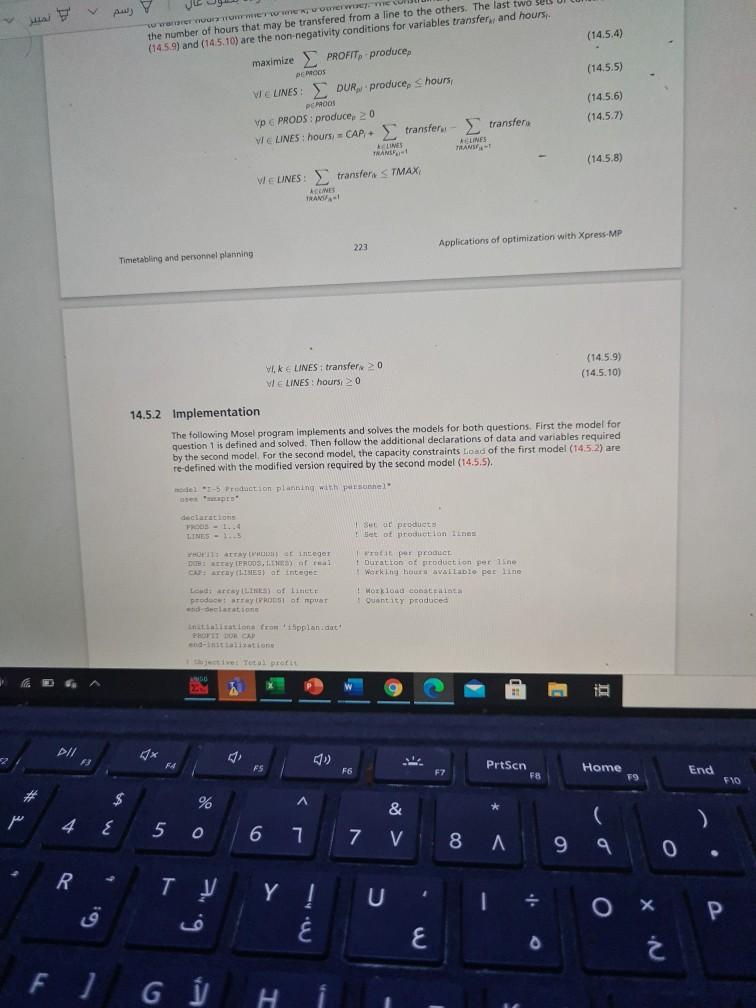
+ * Applications of optimization * Applications of optimisation Application of crimination for C/Users/faisal/Downloads/Applications%20of%20optimization 20with20/press of aus V V B D + A 14.5 Production planning with personnel assignment The company Line Production decides to plan the production of four of its productos five production lines 1 to 5). The company goinnet profits of 67 for the products and 85 P2 and 9 for 13. The maximum time during which the five production lines operate win during the planning period the maximum capacities for 1 to 15 are 4500 hours 5600 hours 1500 hours, and 2500 hours respectively. Table 14,12 lists the processing time in house for production of one unit of every product on every production line. Which quantities off to hold produced to maximize the total profit? subsequently a transfer of personnel and hence of working hours is authorized tym production Applications of options Timetabling and personnel planning Table 14.11: Unitary processing times Lines Products L1 12 14 15 P1 11 0.9 03 09 P2 1 17 14 0.6 1.1 P3 13 12 12 10 P4 0.9 1.1 O 0.9 1.0 Origin LI Table 14.12: Possible transfer of personnel Destination Maximum number of L1 L2 L4 15 transferable hours yes yes no 400 110 yet TO yer 800 yer yes yes min 500 no no 200 ye yen yes ho 300 LA 15 lines during the planning period as shown in Table 14.12, which is the maximum pratit? Howany hours are transfered and under what conditions? 14.5.1 Model formulation Let PRODS be the set of products and LINES the set of production lines. The unit for pis given as PROFIT, and the processing duration of product online DUR The capacity of production line/ in working hours is CAP. As usual in production planning problem, avara indicates the quantity of product that is produced. The model corresponding to the questions fairly simple. The objective is to maximize the total profit (14.5.1) whit remaining within minimalis ENG PII : d) Petsen Hone F FO 17 (2 # $ % r 4 E 5 0 6 77 V 8 A 9 E 2 R Lo P Y E D F ) H J . J Application of optimization Applications of optimization X Applications of optimization X Applications of optimization X BI C:/Users/faisal/Downloads/Applications%20of%20optimization%20with%20Xpress-MP.pdf le + lines during the planning period as shown in Table 14.12, which is the maximum profit7 How many hours are transfered and under what conditions 14.5.1 Model formulation Let PRODS be the set of products and LINES the set of production lines. The per unit profit of product p is given as PROFIT, and the processing duration of product p on line / as DUR The capacity of every production line/ in working hours is CAP. As usual in production planning problems, a variables produce indicates the quantity of product that is produced. The model corresponding to the first question is fairly simple. The objective is to maximize the total profit (14.5.1) whilst remaining within the capacity limits of every production line (constraints (14.5.2)). We obtain the following model: maximize PROFIT, produce (14.5.1) BE (1452) WIELINES: DUR produce, CAP DEMOS Vp PRODS produce, 20 (14.5.3) If it is now possible to transfer personnel from one line to another, variables hours are required that correspond to the working hours used on production line 1. We also introduce variables transfer that represent the number of hours transfered from line I to linek. The constraints (14.5.5) that replace the constraints (14.5.2) of the previous model specify that the number of hours worked is equal to the production multiplied by the per unit duration of the work The constraints (14.5.7) establish the balance between the working hours carried out on a line, the hours transfered and the maximum number of working hours on this line. On one line, hours, hours are worked that correspond to the available nomber of hours for this line, increased by the hours that are transfered to this line from other and decreased by the hours transfered to other lines (TRANSFX is 1 if it is possible to transfer hours from line / to linek, 0 otherwise). The constraints (14.5.8) establish the limits TMAX, on the number of hours that may be transfered from a line to the others. The last two sets of constraints (1459) and (14.5.10) are the non-negativity conditions for variables transfer and hours maximize PROFIT, produce (14.5.4) (14.5.5) WE LINES DUR produce, S hours CODE vp PRODS produce, 20 WIELINES:hours CAP transfer - transfera (14,5,6) (1457) * SURES Leuws TRANS WELINES: transfer STMAX, (1458) Timetasting and personnel planning 221 Aplications of optimization with XpressMP P 1 PI/ x 54 Home End FS PrtScn FB F6 57 79 $10 $ % A 3 p 4 E 50 & C 7 V 8 A 99 6 7 0 Ay Y (14.5.4) (14.5.5) WE WETEN OCH WE me the number of hours that may be transfered from a line to the others. The last two seu (1459) and (145.10) are the non-negativity conditions for variables transfers, and hours maximize PROFITproduce CHOOS WE LINES: DUR, produce. Shours, PCROON Vp E PRODS: produce 2 0 WE LINES: hours, CAPtransfer transferi - transfers ACLINES TRANS TRANI, WE LINES: transfer S TMAX TRAN (14.5.6) (14.5.7) LINES (14.5.8) LE 223 Applications of optimization with Xpress-MP Timetabling and personnel planning WIRELINES: transfer > 0 VI LINES: hours: 0 (1459) (14.5.10) 14.5.2 Implementation The following Mosel program implements and solves the models for both questions. First the model for question 1 is defined and solved. Then follow the additional declarations of data and variables required by the second model. For the second model, the capacity constraints Load of the first model (1452) are re-defined with the modified version required by the second model (14.5.5). model *1-5 Production planning with personnel up declarations FROOS - 1.4 TINES - 15 Sul or products Set of production lines rutat per product 1 Duration of production per line Working hours available per line 11 arranger Day IEROS, CHE (LINES) or Integer Loudrey LLIC) of Li product array ODS of muat declarat ! Workload constanta Quantity produced Initialisations from plan dat PROFIT OR CAP thjective Tutul profit TO PII # x F di 1 FS F6 F7 Prtson F8 Home T9 End FVO * % A $ 4 E & pe 5 0 6 7 7 V ( 8 199 0 R Y o X E F] G / H + * Applications of optimization * Applications of optimisation Application of crimination for C/Users/faisal/Downloads/Applications%20of%20optimization 20with20/press of aus V V B D + A 14.5 Production planning with personnel assignment The company Line Production decides to plan the production of four of its productos five production lines 1 to 5). The company goinnet profits of 67 for the products and 85 P2 and 9 for 13. The maximum time during which the five production lines operate win during the planning period the maximum capacities for 1 to 15 are 4500 hours 5600 hours 1500 hours, and 2500 hours respectively. Table 14,12 lists the processing time in house for production of one unit of every product on every production line. Which quantities off to hold produced to maximize the total profit? subsequently a transfer of personnel and hence of working hours is authorized tym production Applications of options Timetabling and personnel planning Table 14.11: Unitary processing times Lines Products L1 12 14 15 P1 11 0.9 03 09 P2 1 17 14 0.6 1.1 P3 13 12 12 10 P4 0.9 1.1 O 0.9 1.0 Origin LI Table 14.12: Possible transfer of personnel Destination Maximum number of L1 L2 L4 15 transferable hours yes yes no 400 110 yet TO yer 800 yer yes yes min 500 no no 200 ye yen yes ho 300 LA 15 lines during the planning period as shown in Table 14.12, which is the maximum pratit? Howany hours are transfered and under what conditions? 14.5.1 Model formulation Let PRODS be the set of products and LINES the set of production lines. The unit for pis given as PROFIT, and the processing duration of product online DUR The capacity of production line/ in working hours is CAP. As usual in production planning problem, avara indicates the quantity of product that is produced. The model corresponding to the questions fairly simple. The objective is to maximize the total profit (14.5.1) whit remaining within minimalis ENG PII : d) Petsen Hone F FO 17 (2 # $ % r 4 E 5 0 6 77 V 8 A 9 E 2 R Lo P Y E D F ) H J . J Application of optimization Applications of optimization X Applications of optimization X Applications of optimization X BI C:/Users/faisal/Downloads/Applications%20of%20optimization%20with%20Xpress-MP.pdf le + lines during the planning period as shown in Table 14.12, which is the maximum profit7 How many hours are transfered and under what conditions 14.5.1 Model formulation Let PRODS be the set of products and LINES the set of production lines. The per unit profit of product p is given as PROFIT, and the processing duration of product p on line / as DUR The capacity of every production line/ in working hours is CAP. As usual in production planning problems, a variables produce indicates the quantity of product that is produced. The model corresponding to the first question is fairly simple. The objective is to maximize the total profit (14.5.1) whilst remaining within the capacity limits of every production line (constraints (14.5.2)). We obtain the following model: maximize PROFIT, produce (14.5.1) BE (1452) WIELINES: DUR produce, CAP DEMOS Vp PRODS produce, 20 (14.5.3) If it is now possible to transfer personnel from one line to another, variables hours are required that correspond to the working hours used on production line 1. We also introduce variables transfer that represent the number of hours transfered from line I to linek. The constraints (14.5.5) that replace the constraints (14.5.2) of the previous model specify that the number of hours worked is equal to the production multiplied by the per unit duration of the work The constraints (14.5.7) establish the balance between the working hours carried out on a line, the hours transfered and the maximum number of working hours on this line. On one line, hours, hours are worked that correspond to the available nomber of hours for this line, increased by the hours that are transfered to this line from other and decreased by the hours transfered to other lines (TRANSFX is 1 if it is possible to transfer hours from line / to linek, 0 otherwise). The constraints (14.5.8) establish the limits TMAX, on the number of hours that may be transfered from a line to the others. The last two sets of constraints (1459) and (14.5.10) are the non-negativity conditions for variables transfer and hours maximize PROFIT, produce (14.5.4) (14.5.5) WE LINES DUR produce, S hours CODE vp PRODS produce, 20 WIELINES:hours CAP transfer - transfera (14,5,6) (1457) * SURES Leuws TRANS WELINES: transfer STMAX, (1458) Timetasting and personnel planning 221 Aplications of optimization with XpressMP P 1 PI/ x 54 Home End FS PrtScn FB F6 57 79 $10 $ % A 3 p 4 E 50 & C 7 V 8 A 99 6 7 0 Ay Y (14.5.4) (14.5.5) WE WETEN OCH WE me the number of hours that may be transfered from a line to the others. The last two seu (1459) and (145.10) are the non-negativity conditions for variables transfers, and hours maximize PROFITproduce CHOOS WE LINES: DUR, produce. Shours, PCROON Vp E PRODS: produce 2 0 WE LINES: hours, CAPtransfer transferi - transfers ACLINES TRANS TRANI, WE LINES: transfer S TMAX TRAN (14.5.6) (14.5.7) LINES (14.5.8) LE 223 Applications of optimization with Xpress-MP Timetabling and personnel planning WIRELINES: transfer > 0 VI LINES: hours: 0 (1459) (14.5.10) 14.5.2 Implementation The following Mosel program implements and solves the models for both questions. First the model for question 1 is defined and solved. Then follow the additional declarations of data and variables required by the second model. For the second model, the capacity constraints Load of the first model (1452) are re-defined with the modified version required by the second model (14.5.5). model *1-5 Production planning with personnel up declarations FROOS - 1.4 TINES - 15 Sul or products Set of production lines rutat per product 1 Duration of production per line Working hours available per line 11 arranger Day IEROS, CHE (LINES) or Integer Loudrey LLIC) of Li product array ODS of muat declarat ! Workload constanta Quantity produced Initialisations from plan dat PROFIT OR CAP thjective Tutul profit TO PII # x F di 1 FS F6 F7 Prtson F8 Home T9 End FVO * % A $ 4 E & pe 5 0 6 7 7 V ( 8 199 0 R Y o X E F] G / H