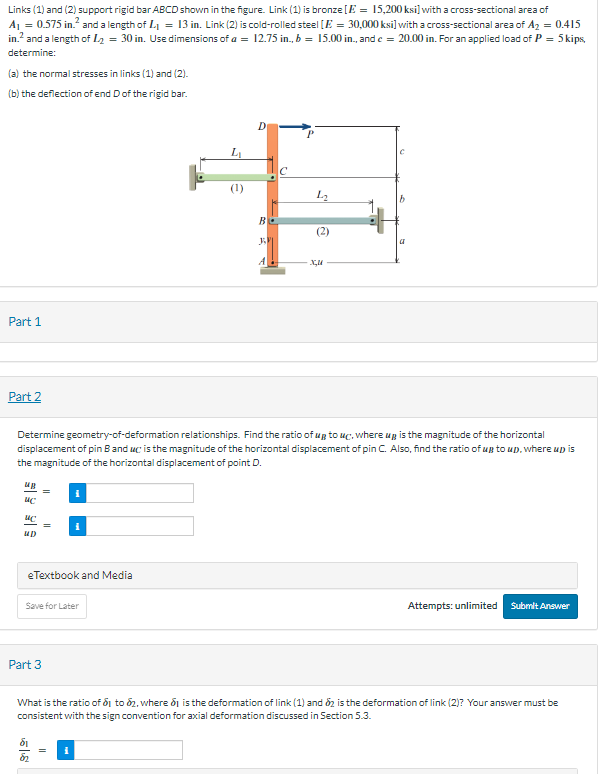
Links $(1)$ and $(2)$ support rigid bar ABCD shown in the figure. Link $(1)$ is bronze $E=15,200$ksi with a cross$-$sectional area of Determine the compatibility equation and use it to find the ratio of $F_1$ to $F_2,$ where $F_1$ is the internal force in link $(1)$ and $F_2$ is the

internal force in link $(2).$ Your answer must be consistent with the sign convention for internal axial forces.

$\frac{F_1}{F_2}=$

eTextbook and Media

Attempts: unlimited

Part $5$

Find the internal forces $F_1$ and $F_2$ in links $(1)$ and $(2),$ respectively. Use the sign convention for internal axial forces.

$F_1=$ kips

$F_2=,1$ kips

kips

Attempts: unlimited

Part $6$

Determine the normal stresses in links $(1)$ and $(2).$ Based on the sign conventions, a tensile normal stress is positive and a

compressive normal stress is negative. Use the sign convention for normal stresses discussed in Section $1\mathrm{.}2.$

${}_1=,1,$ksi

${}_2=,1,$ksi

eTextbook and Media

Part $7$

Determine the deflection of link $(1).$ Use the sign convention for axial deformation.

${}_1=$ Part $8$

Determine the deflection of end $D$ of the rigid bar. Enter a positive value if it deflects to the right, or a negative value if it deflects

to the left.

$uD=$

i

in$.$

$A_1=0\mathrm{.}575i{n}^2$ and a length of $L_1=13in.$ Link $(2)$ is cold$-$rolled steel $E=30,000$ksi with a cross$-$sectional area of $A_2=0\mathrm{.}415$

in$.{?}^2$ and a length of $L_2=30in.$ Use dimensions of $a=12\mathrm{.}75in.,b=15\mathrm{.}00in.,$ and $c=20\mathrm{.}00in.$ For an applied load of $P=5$kips,

determine:

$($a$)$ the normal stresses in links $(1)$ and $(2).$

$($b$)$ the deflection of end $D$ of the rigid bar.

Part $1$

Part $2_{?}$

Determine geometry$-$of$-$deformation relationships. Find the ratio of $u_B$ to $u_C,$ where $u_B$ is the magnitude of the horizontal

displacement of pin $B$ and $uC$ is the magnitude of the horizontal displacement of pin $C.$ Also, find the ratio of $u_B$ to $u_D,$ where $uD$ is

the magnitude of the horizontal displacement of point $D.$

$\frac{u_B}{u_C}=1$

$\frac{u_C}{u_D}=1$

eTextbook and Media

Attempts: unlimited

Part $3$

What is the ratio of ${}_1$ to ${}_2,$ where ${}_1$ is the deformation of link $(1)$ and ${}_2$ is the deformation of link $(2)?$ Your answer must be

consistent with the sign convention for axial deformation discussed in Section $5\mathrm{.}3.$

$\frac{{}_1}{{}_2}=$