Looking for short concise answers

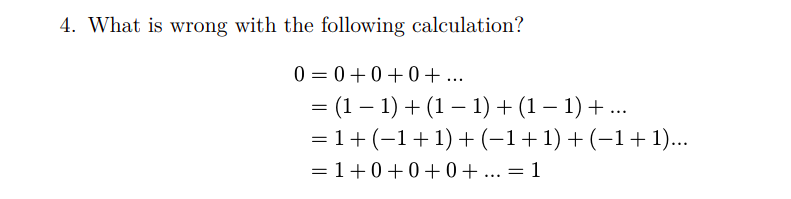
1. Give an example for each of the following: (a) a sequence that is not eventually monotonic but converges (b) a decreasing sequence without a limit (c) a bounded sequence without a limit 4. What is wrong with the following calculation? 0 = 0+0+0+... = (1 - 1) + (1 - 1) +(1 -1) + ... =1+ (-1+1)+ (-1+1) + (-1+1) ... =1+0+0+0+ ...=13. Consider the following two series: _ 2\\/ (4n)! (1103 + 263901;). 31 Z 0(411 + 1)( (4n. + 3) 32 9801 n; (n!)43964\" It turns out that 31 = w/4 (a result irom around 1676 attributed to Gottfried Leibniz) and S: = 1/11- (a result from around 1910 attributed to Srinivasa Ramanujan). Let us suppose that we want to estimate the value of it. How many correct decimal places of 51 do you get by using (a) one and (b) two terms of each of these series (you can try higher number of terms using e.g., Wolfram Alpha)? Based on your observations, which of these two series would you choose to approximate '31" and why? Note: you should be able to show that these two series actually converge (no need to show your work for this). 2. In this question, {on}ff=1 is a sequence of real numbers: (a) Let N be a positive integer. What is the difference between the following? . . N 1. 11111 on 11-100 111. E an 11:] N no ii. ]iTIL :51 iv. 2 Nioo '11 an