$M_1*x_1^{}+D_1*x_1^{}-D_1{x}_2^{}+K_1{x}_1=0$

$M_2{x}_2^{}+D_1{x}_2^{}-D_1{x}_1^{}+K_2{x}_2-K_2{x}_3=u(t)$

$M_3{x}_3^{}+D_2{x}_3^{}-K_2{x}_3-K_2{x}_2=0$

$x_1^{}=\frac{-D_1{x}_1^{}+D_1{x}_2^{}{k}_1{x}_1}{M_1}$

$x_2^{}=u(t)-\frac{D_1{x}_2^{}+D_1{x}_1^{}-K_2{x}_2+K_2{x}_3}{M_2}$

$x_3^{}=\frac{-D_2{x}_3^{}+K_2{x}_3+K_2{x}_2}{M_3}$

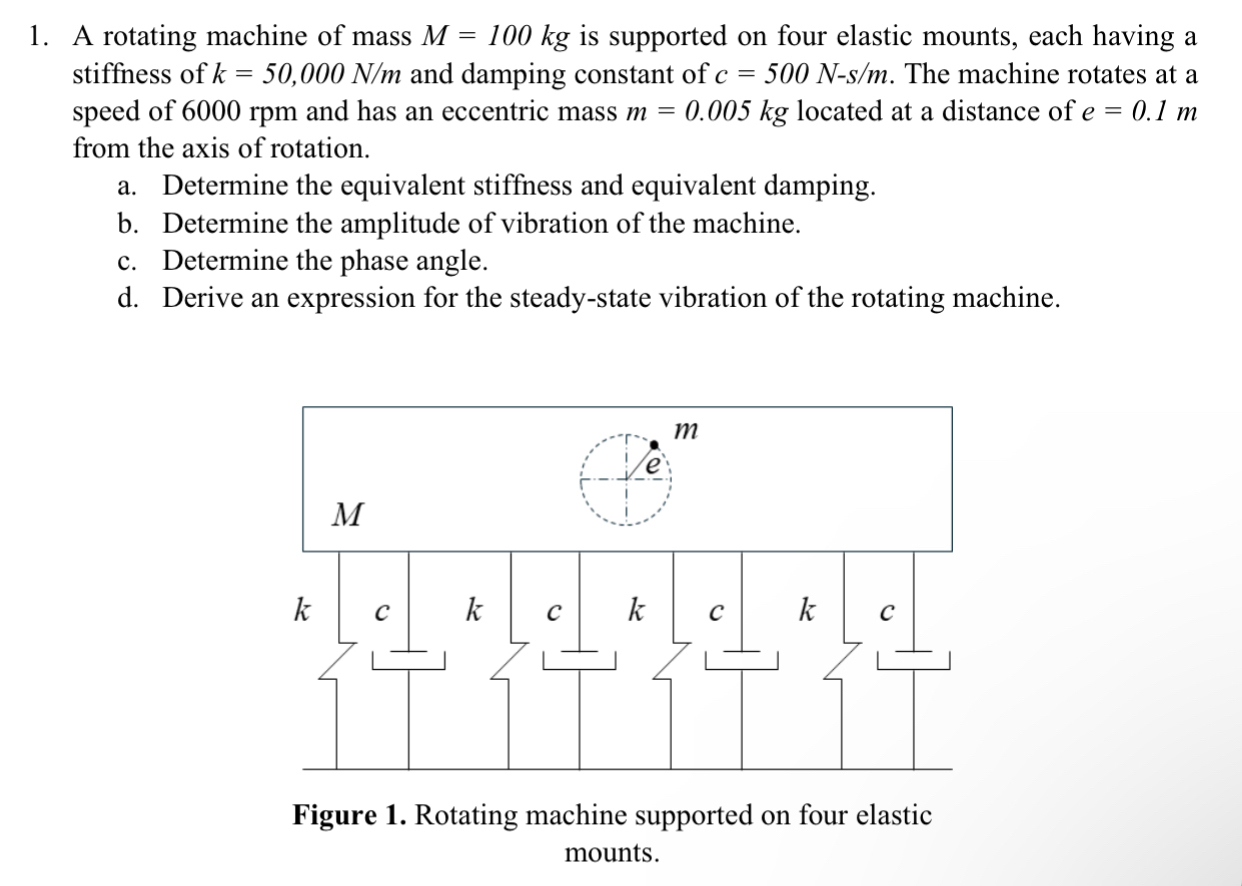
A rotating machine of mass $M=100kg$ is supported on four elastic mounts, each having a stiffness of $k=50,000\frac{N}{m}$ and damping constant of $c=500N-\frac{s}{m}.$ The machine rotates at a speed of $6000$ rpm and has an eccentric mass $m=0\mathrm{.}005kg$ located at a distance of $e=0\mathrm{.}1m$ from the axis of rotation.

a$.$ Determine the equivalent stiffness and equivalent damping.

b$.$ Determine the amplitude of vibration of the machine.

c$.$ Determine the phase angle.

d$.$ Derive an expression for the steady$-$state vibration of the rotating machine.

Figure $1.$ Rotating machine supported on four elastic mounts.