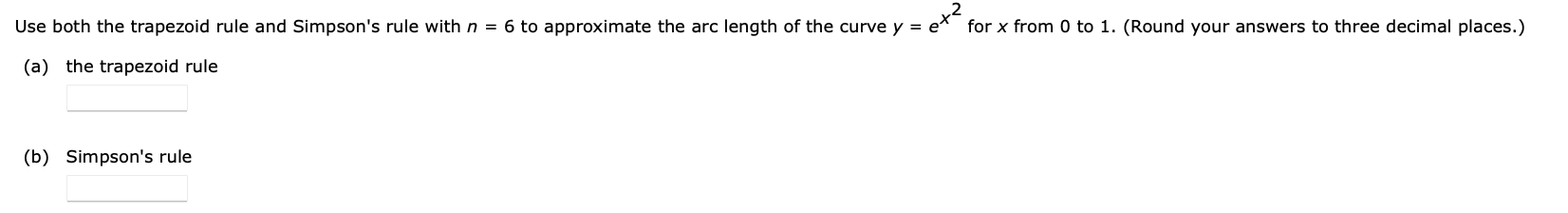
MA 2.5:

1)

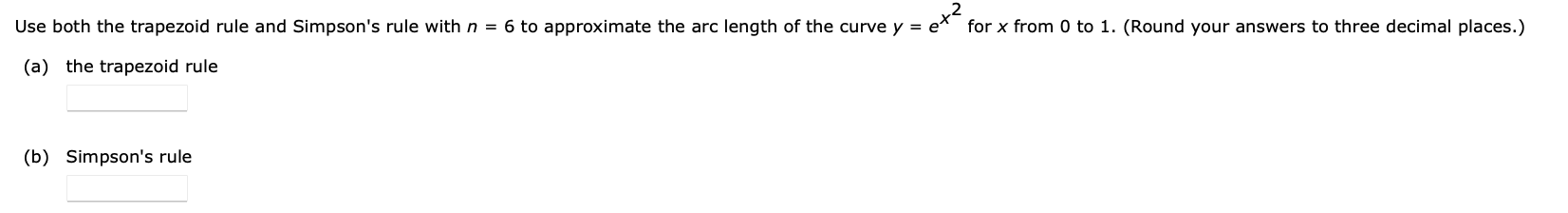
Approximate the definite integral using the trapezoidal rule for the given value of n. Give the result accurate to 3 decimal places. 11 dx (a) n = 8 /3 1 +x (b) Find the upper bound for the absolute value of the error based on If"(x) | and Theorem 1. (Round your answer to three decimal places.) (c) Find the exact value of the definite integral.Approximate the definite integral using the trapezoidal rule for the given value of n. Give the result accurate to 3 decimal places. (a) sin(x) dx n = 6 (b) Find the upper bound for the absolute value of the error based on If"(x) | and Theorem 1. LETIS (c) Find the exact value of the definite integral.Approximate the definite integral using the trapezoidal rule for the given value of n. Give the result accurate to 3 decimal places. (This exercise cannot be integrated using our usual methods.) 9 2 /|n(1+x )dx n=4 .8 Approximate the definite integral using Simpson's rule for the given value of n. Give the result accurate to 3 decimal places. (a) 1 dx n = 8 2 x+1 (b) Find the upper bound for the absolute value of the error based on If()(x) | and Theorem 2. (Round the decimal value to three decimal places.) |Esl S x 10-6 (c) Find the exact value of the definite integral.Approximate the definite integral using Simpson's rule for the given value of n. Give the result accurate to 3 decimal places. . 1/ 2 (a) sin(x) dx n = 6 (b) Find the upper bound for the absolute value of the error based on If()(x) | and Theorem 2. (Round your answer to three decimal places.) IEsl S (c) Find the exact value of the definite integral.Approximate the definite integral using Simpson's rule for the given value of n. Give the result accurate to 3 decimal places. (This exercise cannot be integrated using our usual methods.) 6 2 /e_x dx n:6 .0 2 Use both the trapezoid rule and Simpson's rule with n = 6 to approximate the arc length of the curve y = ex for x from D to 1. (Round your answers to three decimal places.) (a) the trapezoid rule (b) Simpson's rule The velocity v, in meters per second, of an object at time t, in seconds, is given in the table below. t 0 0.5 1 1.5 2 2.5 3 v(t) 5.4 5.7 6.2 6.7 7.2 6.8 6.1 Use the trapezoidal rule to approximate the distance s, in meters, traveled by the object from t = 0 to t = 3