Machine Epsilon True Errors in Storage of Binary Numbers Question in Picture Below. Thank you.

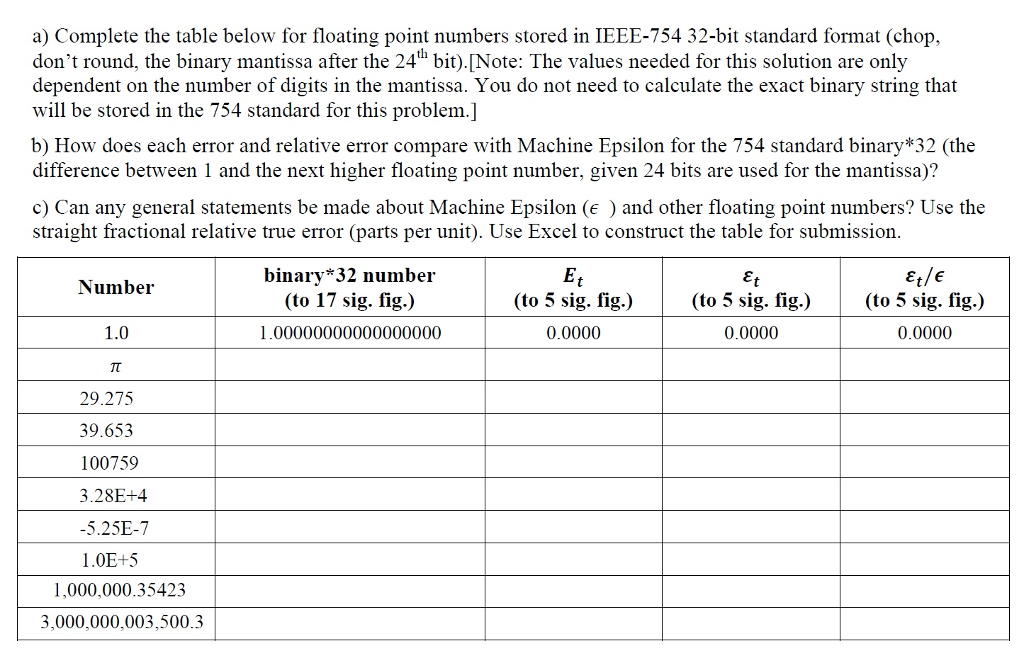
a) Complete the table below for floating point numbers stored in IEEE-754 32-bit standard format (chop, don't round, the binary mantissa after the 24th bit).[Note: The values needed for this solution are only dependent on the number of digits in the mantissa. You do not need to calculate the exact binary string that will be stored in the 754 standard for this problem.] b) How does each error and relative error compare with Machine Epsilon for the 754 standard binary*32 (the difference between 1 and the next higher floating point number, given 24 bits are used for the mantissa)? c) Can any general statements be made about Machine Epsilon (e ) and other floating point numbers? Use the straight fractional relative true error (parts per unit). Use Excel to construct the table for submission. Et Et Et/e Number binary*32 number (to 17 sig. fig.) 1.00000000000000000 (w 5 ili ne) (u svi racu s viac na (to 5 sig. fig.) (to 5 sig. fig.) 0.0000 (to 5 sig. fig.) 0.0000 1.0 0.0000 29.275 39.653 100759 3.28E+4 -5.25E-7 1.0E+5 1,000,000.35423 3,000,000,003,500.3 a) Complete the table below for floating point numbers stored in IEEE-754 32-bit standard format (chop, don't round, the binary mantissa after the 24th bit).[Note: The values needed for this solution are only dependent on the number of digits in the mantissa. You do not need to calculate the exact binary string that will be stored in the 754 standard for this problem.] b) How does each error and relative error compare with Machine Epsilon for the 754 standard binary*32 (the difference between 1 and the next higher floating point number, given 24 bits are used for the mantissa)? c) Can any general statements be made about Machine Epsilon (e ) and other floating point numbers? Use the straight fractional relative true error (parts per unit). Use Excel to construct the table for submission. Et Et Et/e Number binary*32 number (to 17 sig. fig.) 1.00000000000000000 (w 5 ili ne) (u svi racu s viac na (to 5 sig. fig.) (to 5 sig. fig.) 0.0000 (to 5 sig. fig.) 0.0000 1.0 0.0000 29.275 39.653 100759 3.28E+4 -5.25E-7 1.0E+5 1,000,000.35423 3,000,000,003,500.3