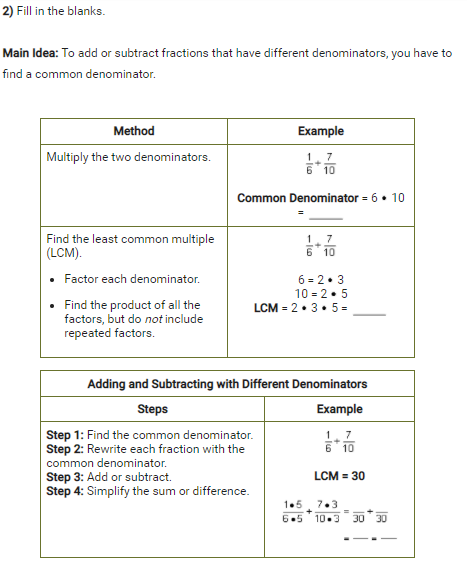
Main Idea: Adding or subtracting rational expressions with common denominators is just like adding or subtracting fractions with common denominators. Fractions Rational expressions b_a+b C C C C C C Adding and Subtracting with Common Denominators Steps Fraction Rational expression example example Step 1: Add the 1 1 2+1 X 4 9 9 x - 5 x - 5 x - 5 Step 2: Keep the common Step 3: Simplify the sum 4 - X X - (4 - x) or difference X - 5 X - 5 X - 5 Step 4: List any values 2-3 X - 4+x of the variable that X - 5 make the expression undefined. where x * 52) Fill in the blanks. Main Idea: To add or subtract fractions that have different denominators, you have to find a common denominator. Method Example Multiply the two denominators. 1 7 6 10 Common Denominator = 6 * 10 Find the least common multiple 1 7 (LCM). 6 10 . Factor each denominator. 6 = 2. 3 10 = 2 - 5 Find the product of all the LCM = 2 . 3 . 5= factors, but do not include repeated factors. Adding and Subtracting with Different Denominators Steps Example Step 1: Find the common denominator. 1 7 Step 2: Rewrite each fraction with the 6 10 common denominator. Step 3: Add or subtract. LCM = 30 Step 4: Simplify the sum or difference. 1 5 7.3 6.5 10-3 30 303) Fill in the blanks. Main Idea: Adding or subtracting rational expressions with different denominators is just like adding or subtracting fractions with different denominators. Steps Example: 7 x - 2x -3 x +x Step 1: Find the common denominator. x -2x - 3 - (x- 3)_ x+ x= x LCM = x(x - 3)(x+1) Step 2: Rewrite each fraction with the 7 1 X - 3 common denominator. ( x - 3) (x + 1] X MX+1] x-3 M(x+ 1) (X-3) MX+ 1(x-3) Step 3: Add or subtract. 7 x - (x- 3) (Be careful to subtract every term in the x(x + 1)(x -3) subtracted polynomial - distribute the minus sign.) 7x- + x(x + 1(x-3) Step 4: Simplify the sum or difference. x( x + 1)(x - 3) Step 5: List any values of the variable X - that make the expression undefined