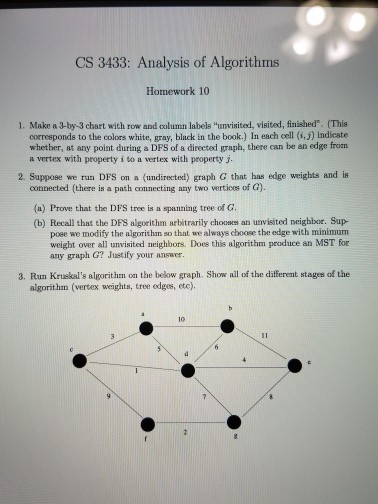
Make a 3-by-3 chart with row and column labels "unvisited, visited, finished". (This corresponds to the colors white, gray, black in the book.) In each cell (i, j) indicate whether, at any point during a DFS of a directed graph, there can be an edge from a vertex with property i to a vertex with property j. Suppose we run DFS on a (undirected) graph G that has edge weights and is connected (there is a path connecting any two vertices of G). (a) Prove that the DFS tree is a spanning tree of G. (b) Recall that the DFS algorithm arbitrarily chooses an unvisited neighbor. Suppose we modify the algorithm so that we always choose the edge with minimum weight over all unvisited neighbors. Does this algorithm produce an MST for any graph G? Justify your answer. Run Kruskal's algorithm on the below graph. Show all of the different stages of the algorithm (vertex weights, tree edges, etc)