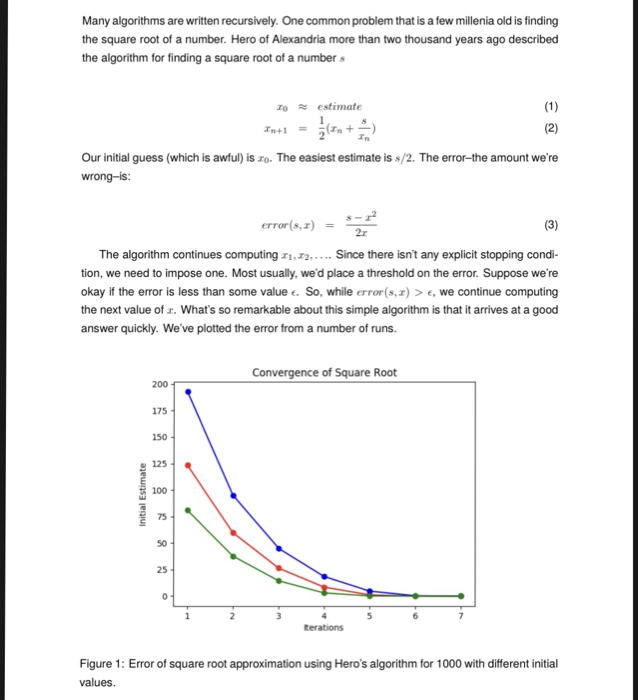
Many algorithms are written recursively. One common problem that is a few millenia old is finding the square root of a number. Hero of Alexandria more than two thousand years ago describecd the algorithm for finding a square root of a number s To estimate Our initial guess (which is awful) is ro. The easiest estimate is s/2. The error-the amount we're error(s,z) The algorithm continues computing i,2....Since there isn't any explicit stopping condi- tion, we need to impose one. Most usually, we'd place a threshold on the error. Suppose we're okay if the error is less than some value e. So, while error(s,x) > , we continue computing the next value of r. What's so remarkable about this simple algorithm is that it arrives at a good answer quickly. We've plotted the error from a number of runs. Convergence of Square Root 200 175 150 125 100 75 50 Figure 1: Error of square root approximation using Hero's algorithm for 1000 with different initial Many algorithms are written recursively. One common problem that is a few millenia old is finding the square root of a number. Hero of Alexandria more than two thousand years ago describecd the algorithm for finding a square root of a number s To estimate Our initial guess (which is awful) is ro. The easiest estimate is s/2. The error-the amount we're error(s,z) The algorithm continues computing i,2....Since there isn't any explicit stopping condi- tion, we need to impose one. Most usually, we'd place a threshold on the error. Suppose we're okay if the error is less than some value e. So, while error(s,x) > , we continue computing the next value of r. What's so remarkable about this simple algorithm is that it arrives at a good answer quickly. We've plotted the error from a number of runs. Convergence of Square Root 200 175 150 125 100 75 50 Figure 1: Error of square root approximation using Hero's algorithm for 1000 with different initial