Many forecasting models use parameters that are estimated using nonlinear optimization. A good example is the Bass model introduced in this chapter. Another example is the exponential smoothing forecasting model. The exponential smoothing model is common in practice. For instance, the basic exponential smoothing model for forecasting sales is

hat$(y{)}_{t+1}=a{y}_t+(1-a)hat(y{)}_t$

where

hat$(y{)}_{t+1}=$ forecast of sales for period $t+1$

$y_t=$ actual value of sales for period $t$

hat$(y{)}_t=$ forecast of sales for period $t$

$a=$ smoothing constant $0a1.$

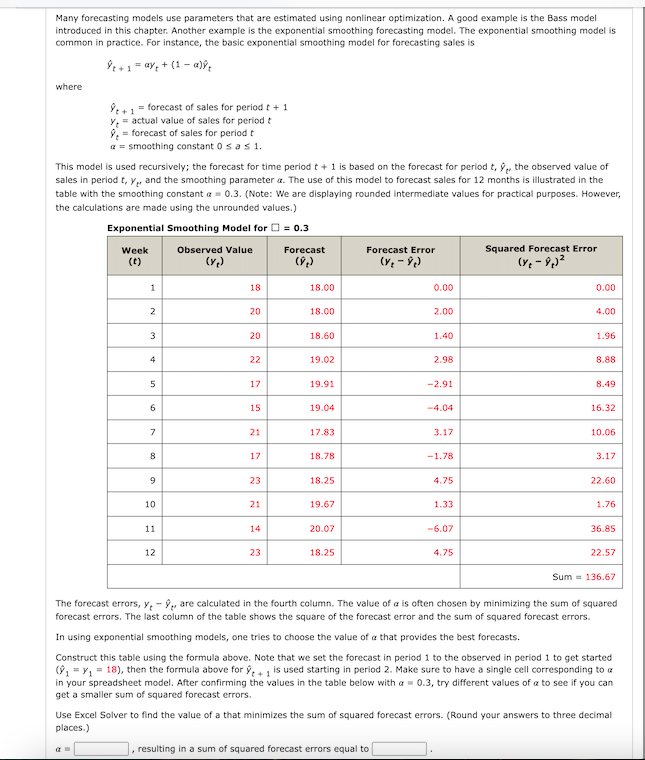
This model is used recursively; the forecast for time period $t+1$ is based on the forecast for period $t,$hat$(y{)}^{\text{'}},$ the observed value of sales in period $t,y_l,$ and the smoothing parameter $.$ The use of this model to forecast sales for $12$ months is illustrated in the table with the smoothing constant $=0\mathrm{.}3.($Note: We are displaying rounded intermediate values for practical purposes. However, the calculations are made using the unrounded values.$)$

Exponential Smoothing Model for $=0\mathrm{.}3$

$\backslash$table$[[\backslash$table$[[$Week$],[($t$)]],\backslash$table$[[$Observed Value$],[($y$\_($t$))]],\backslash$table$[[$Forecast$],[($hat$($y$)\_($t$))]],\backslash$table$[[$Forecast Error$],[($y$\_($t$)-$hat$($y$)\_($t$))]],\backslash$table$[[$Squared Forecast Error$],[($y$\_($t$)-$hat$($y$)\_($t$))^(2)]]],[1,18,18\mathrm{.}00,0\mathrm{.}00,0\mathrm{.}00],[2,20,18\mathrm{.}00,2\mathrm{.}00,4\mathrm{.}00],[3,20,18\mathrm{.}60,1\mathrm{.}40,1\mathrm{.}96],[4,22,19\mathrm{.}02,2\mathrm{.}98,8\mathrm{.}88],[5,17,19\mathrm{.}91,-2\mathrm{.}91,8\mathrm{.}49],[6,15,19\mathrm{.}04,-4\mathrm{.}04,16\mathrm{.}32],[7,21,17\mathrm{.}83,3\mathrm{.}17,10\mathrm{.}06],[8,17,18\mathrm{.}78,-1\mathrm{.}78,3\mathrm{.}17],[9,23,18\mathrm{.}25,4\mathrm{.}75,22\mathrm{.}60],[10,21,19\mathrm{.}67,1\mathrm{.}33,1\mathrm{.}76],[11,14,20\mathrm{.}07,-6\mathrm{.}07,46\mathrm{.}85],[12,23,18\mathrm{.}25,,22\mathrm{.}57],[,,,,136\mathrm{.}67]]$

The forecast errors, $y_t-$hat$(y{)}_t,$ are calculated in the fourth column. The value of $$ is often chosen by minimizing the sum of squared forecast errors. The last column of the table shows the square of the forecast error and the sum of squared forecast errors.

In using exponential smoothing models, one tries to choose the value of a that provides the best forecasts.

Construct this table using the formula above. Note that we set the forecast in period $1$ to the observed in period $1$ to get started $(hat(y{)}_1=y_1=18),$ then the formula above for hat$(y{)}_{t+1}$ is used starting in period $2.$ Make sure to have a single cell corresponding to $a$ in your spreadsheet model. After confirming the values in the table below with $=0\mathrm{.}3,$ try different values of $$ to see if you can get a smaller sum of squared forecast errors.

Use Excel Solver to find the value of a that minimizes the sum of squared forecast errors. $($Round your answers to three decimal places.$)$

$=$

$,$ resulting in a sum of squared forecast errors equal to