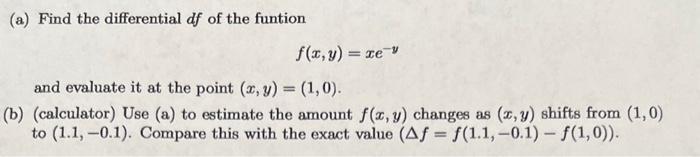
Many physical phenomena are modeled by partial differential equations, or equations involving partial derivatives. The simplest example is the transport equation: u u + c t = 0 (1) which models a wave moving at a constant speed c without changing its shape. u(x, t) represents the height of the wave at point x and time t. A solution of the transport equation is any function u(x, t) for which Eq. (1) is a true statement. (a) Verify that u(x, t) = sin(x- ct) is a solution of the transport equation. (b) Verify that u(x, t) = e-(-ct) is a solution of the transport equation. (a) Find the differential df of the funtion f(z,M) = xe * and evaluate it at the point (x, y) = (1,0). (b) (calculator) Use (a) to estimate the amount f(x, y) changes as (x, y) shifts from (1,0) to (1.1, -0.1). Compare this with the exact value (Af = f(1.1,-0.1) - (1,0)).