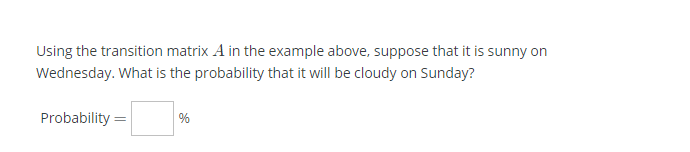
Markov Matrices Markov Matrices. also known as Markov Chains. are used to model systems (or processes} that evolve through a series of stages. At each stage. the system is in one of a nite number of states. Example 7.36: Simplied Weather Model On any particular day. the weather is said to occupy one of three possible states: sunny (5}. cloudy {C}. or rainy {R}. In this case. the stages are the days. The state that the system occupies at any stage is determined by a set of probabilities. Important fact: probabilities are always real numbers between zero and one. inclusive. Due to this. Markov Matrices have columns made up of nonnegative numbers that sum to one. - If it is sunny one day. then there is a 40% chance it will be sunny the next day. and a 40% chance that it will be cloudy the next day {and a 20% chance it will be rainythe next day}. The values 40%. 40% and 20% are transition probabilities. and are assumed to be known. 0 If it is cloudy one day. then there is a 40% chance it will be rainy the next day, and a 25% chance that it will be sunny the next day. 0 If it is rainy one day. then there is a 30% chance it will be rainy the next day, and a 50% chance that it will be cloudy the next day. We put the transition probabilities into a transition matrix, 'ITO' OJ 53 0-'2 A M 0.! 0.!- |h 0.! M In Note. A transition matrix is an example of a stochastic. meaning a matrix with the property thatthe sum ofthe entries in each column is equal to one. Suppose that it is rainy on Thursday. what is the probability that it will be sunny on Sunday? The initial state vector. X0. corresponds to the state of the weather on Thursday. so 05 Xu=0 c In First, the state vector for Friday is 0.2 0.4 0.25 0.2 0 X1: 0.5 = 0.4 0.35 0.5 0 =A_Xn. 0.3 0.2 0.4 0.3 1 Next. the state vector for Saturday is 0.4 0.25 0.2 0.2 0.205 X5 = AX] = 0.4 0.35 0.5 0.5 = 0.405 0.2 0.4 0.3 0.3 0.33 Finally. the state vector for Sunday is 0.4 0.25 0.2 0.265 0.27325 X3 = AXQ = 0.4 0.35 0.5 0.405 = 0.41275 0.2 0.4 0.3 0.33 0.314 Therefore. the probability that it will be sunny on Sunday is 27.32596. Using the transition matrix A in the example above, suppose that it is sunny on Wednesday. What is the probability that it will be cloudy on Sunday? Probability = %