Markowitz portfolio optimization: Harry Markowitz received the 1990 Nobel Prize for his path-breaking work in portfolio optimization. One version of the Markowitz model is based on minimizing the variance of the portfolio subject to a constraint on return. The below table shows the annual return (%) for five 1-year periods for the six mutual funds with the last row that gives the S&P 500 return for each planning scenario. Scenario 1 represents a year in which the annual returns are good for all the mutual funds. Scenario 2 is also a good year for most of the mutual funds. But scenario 3 is a bad year for the small-cap value fund; scenario 4 is a bad year for the intermediate-term bond fund; and scenario 5 is a bad year for four of the six mutual funds.

Mutual Fund	Scenario 1	Scenario 2	Scenario 3	Scenario 4	Scenario 5
Foreign Stock	10.06	13.12	13.47	45.42	-21.93
Intermediate-Term Bond	17.64	3.25	7.51	-1.33	7.36
Large-Cap Growth	32.41	18.71	33.28	41.46	-23.26
Large-Cap Value	32.36	20.61	12.93	7.06	-5.37
Small-Cap Growth	33.44	19.40	3.85	58.68	-9.02
Small-Cap Value	24.56	25.32	-6.70	5.43	17.31
S&P 500 Return	25.00	20.00	8.00	30.00	-10.00

If each of the scenarios is equally likely and occurs with probability 1/5, then the mean return or expected return of the portfolio is

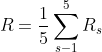
The variance of the portfolio return is

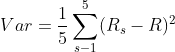
Using the scenario return data given in Table above, the Markowitz mean-variance model can be formulated. The objective function is the variance of the portfolio and should be minimized. Assume that the required return on the portfolio is 10%. There is also a unity constraint that all of the money must be invested in mutual funds.

Most investors are happy when their returns are "above average," but not so happy when they are "below average." In the Markowitz portfolio optimization model given above, the objective function is to minimize variance, which is given by

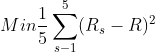
where R_s is the portfolio return under scenario s and R is the expected or average return of the portfolio.

With this objective function, we are choosing a portfolio that minimizes deviations both above and below the average, R. However, most investors are happy when R_s > R, but unhappy when R_s R. With this preference in mind, an alternative to the variance measure in the objective function for the Markowitz model is the semivariance. The semivariance is calculated by only considering deviations below R.

Let D_sp - D_sn - R_s - R and restrict D_sp and DD_sn to be nonnegative. Then D_sp measures the positive deviation from the mean return in scenario s (i.e., DD_sp = R_s - R when R_s R)

In the case where the scenario return is below the average return, R_s R, we have - D_sn = R_s - R. Using these new variables, we can reformulate the Markowitz model to only minimize the square of negative deviations below the average return. By doing so, we will use the semivariance rather than the variance in the objective function.

Solve the Markowitz portfolio optimization model that can be prepared for above case to use semivariance in the objective function. Solve the model using Excel Solver. If required, round your answers to one decimal place.

Mutual Funds	Investments in %
Foreign Stock	%
Intermediate-Term Bond	%
Large-Cap Growth	%
Large-Cap Value	%
Small-Cap Growth	%
Small-Cap Value	%

- L3 - Var - R) 1 Min(R, - R) - L3 - Var - R) 1 Min(R, - R)