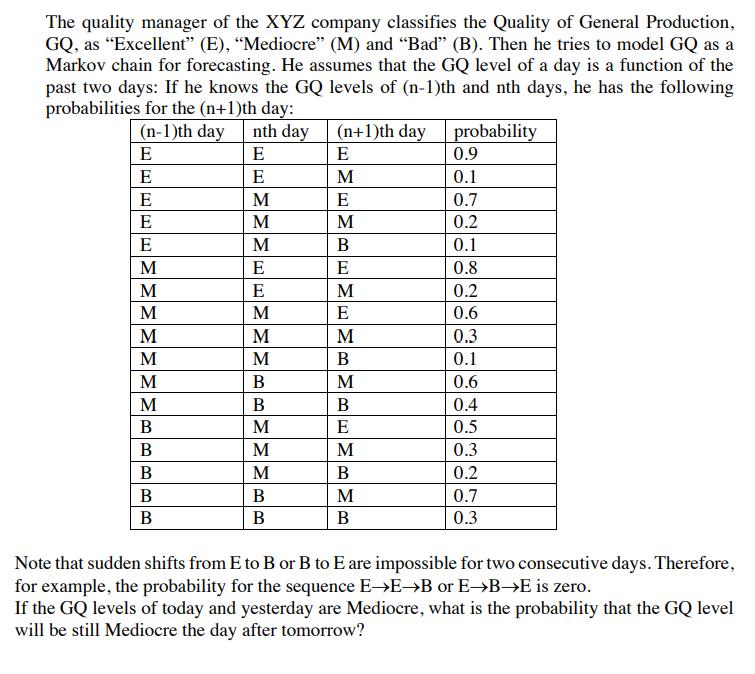
The quality manager of the XYZ company classifies the Quality of General Production, GQ, as "Excellent" (E), "Mediocre" (M) and "Bad" (B). Then he tries to model GQ as a Markov chain for forecasting. He assumes that the GQ level of a day is a function of the past two days: If he knows the GQ levels of (n-1)th and nth days, he has the following probabilities for the (n+1)th day: (n-1)th day E E EEEMM M M M M M B B BB B nth day E E M M M E E M M M B B M M M B B (n+1)th day E M E M B E M E M B M B E M B M B probability 0.9 0.1 0.7 0.2 0.1 0.8 0.2 0.6 0.3 0.1 0.6 0.4 0.5 0.3 0.2 0.7 0.3 Note that sudden shifts from E to B or B to E are impossible for two consecutive days. Therefore, for example, the probability for the sequence EEB or EBE is zero. If the GQ levels of today and yesterday are Mediocre, what is the probability that the GQ level will be still Mediocre the day after tomorrow?