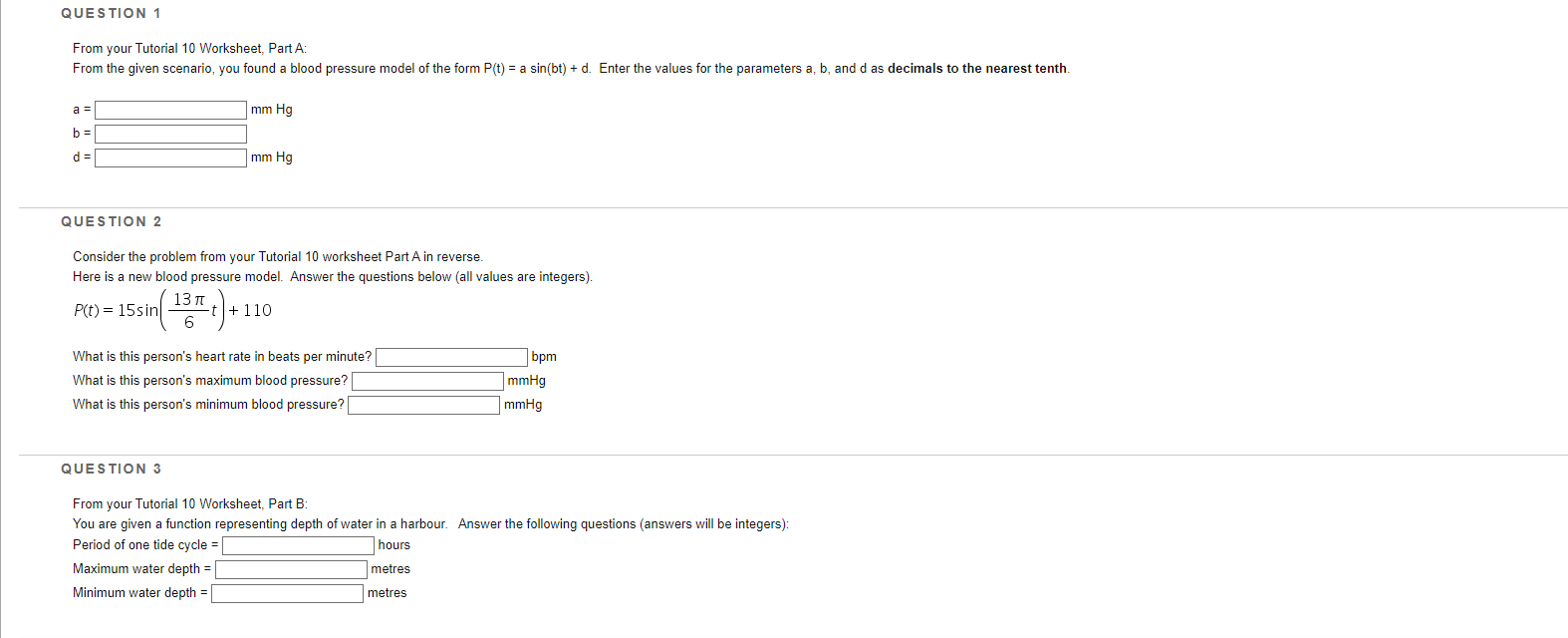
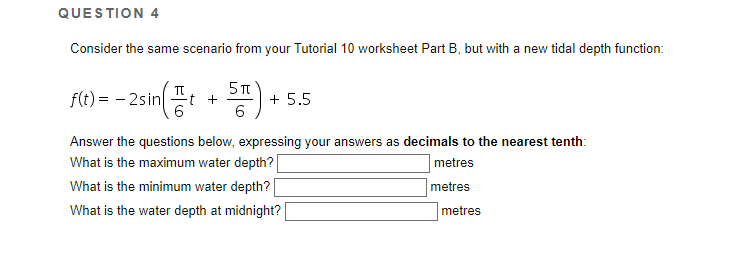
Question: Math 0130 Tutorial 10 A Finding a Blood Pressure Model (Assume No Phase Shift) A hypertensive person has a pulse rate of 80 heartbeats per

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


