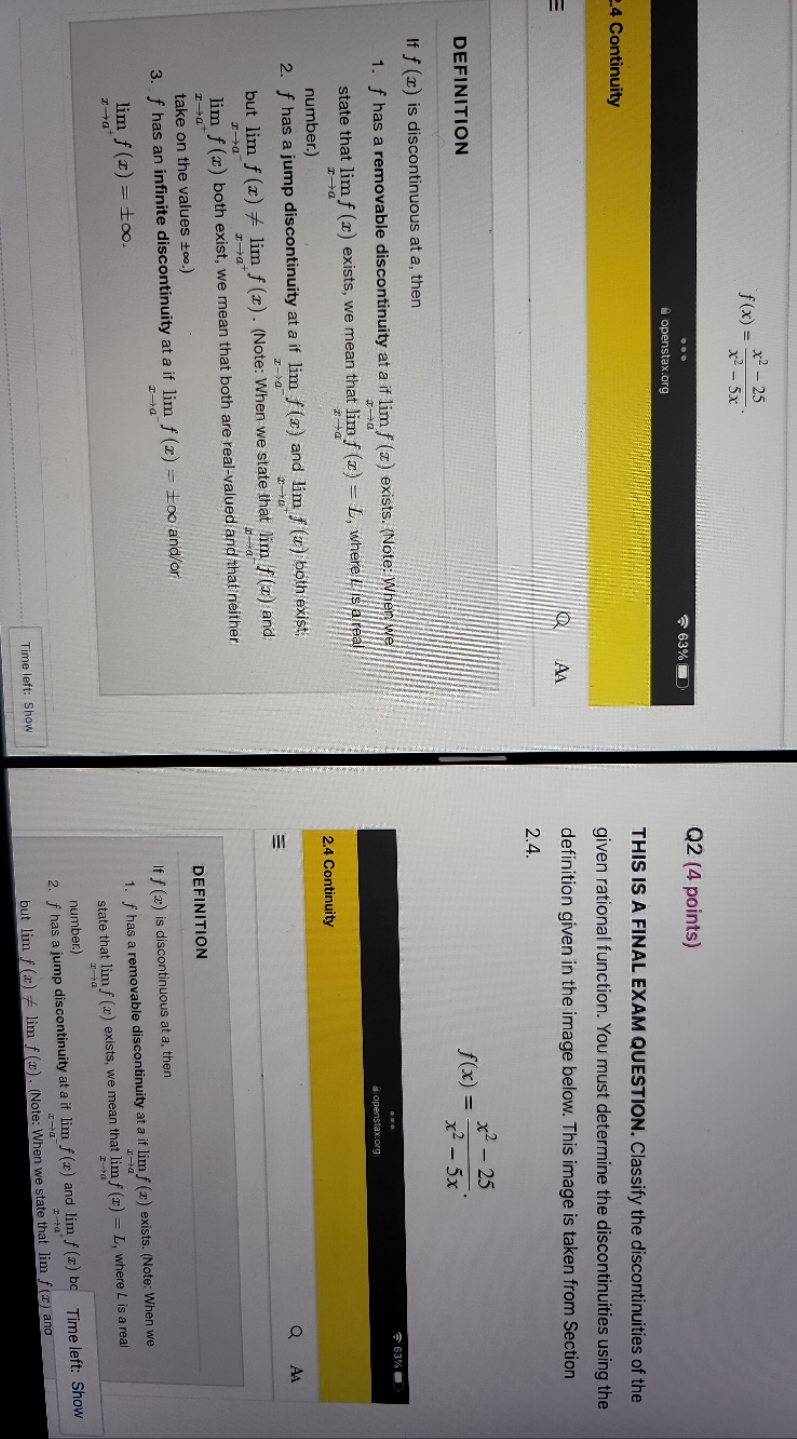
Math Calculus 110 pls answer with numbers showing the work as math work, not by just writing as words to just explain. pls write on paper with normal clear handwriting. pls be clear when writing it down and show the step by step. thank you! NOTE: This is ONE question it's the same question it's just on a divided screen to show the quetion better

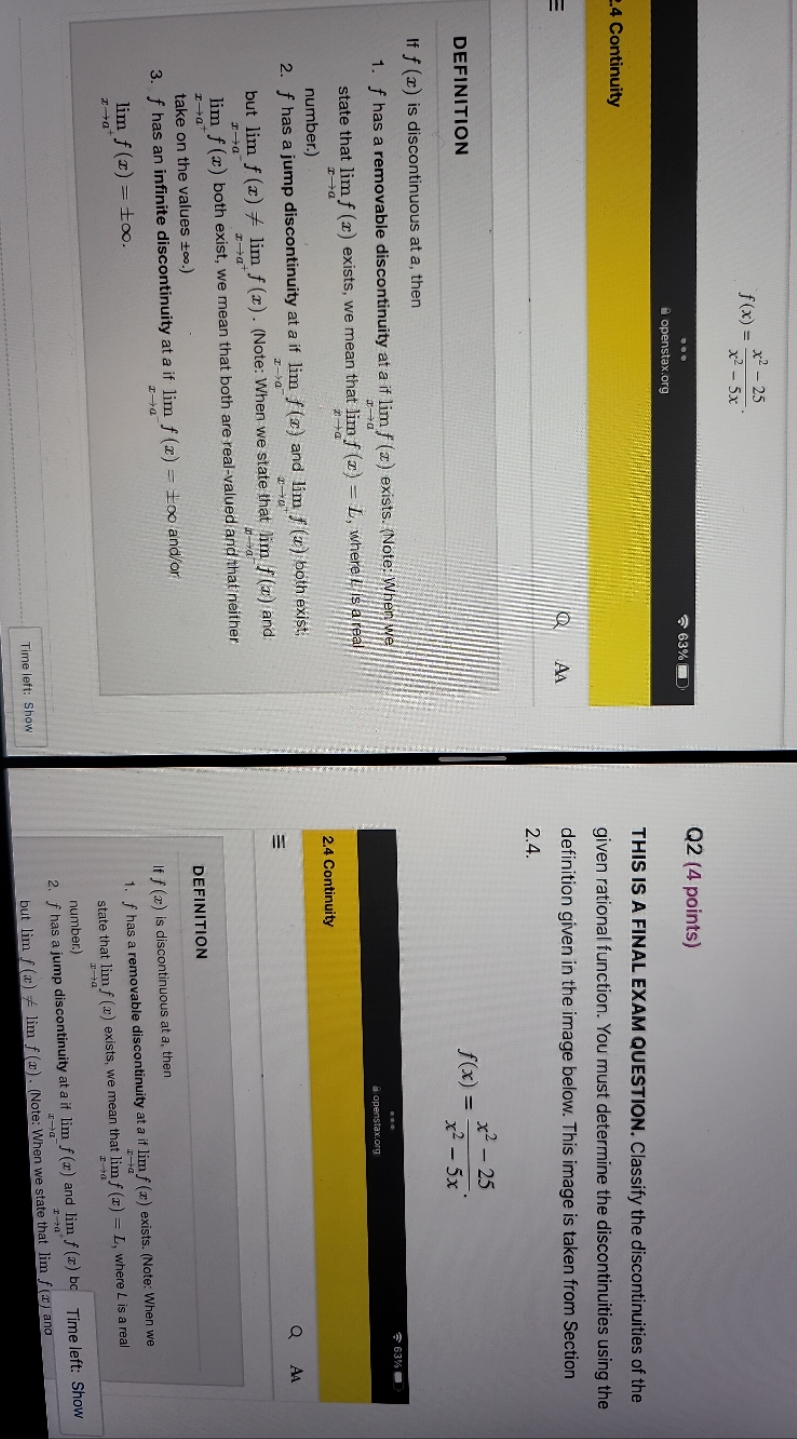
f (x) = x2 - 25 x 2 - 5x . .. 63% Q2 (4 points) A openstax.org 4 Continuity THIS IS A FINAL EXAM QUESTION. Classify the discontinuities of the given rational function. You must determine the discontinuities using the definition given in the image below. This image is taken from Section 2.4. DEFINITION f (x ) = x 2 - 25 x2 - 5x If f (x) is discontinuous at a, then 1. f has a removable discontinuity at a if lim f (x ) exists. (Note: When we a a . .. 63 state that lim f (x) exists, we mean that lim f (z) = L, where I is a real openstax.org r-+a number.) 2.4 Continuity 2. f has a jump discontinuity at a if lim f (x) and lim f (x) both exist, o AA but lim f (x) * lim f (x) . (Note: When we state that lim f (x) and lim f (x) both exist, we mean that both are real-valued and that neither take on the values co.) DEFINITION 3. f has an infinite discontinuity at a if lim f (x) = 100 and/or I-+a If f (x) is discontinuous at a, then lim f (x) = 100. z-a 1. f has a removable discontinuity at a if lim f (x) exists. (Note: When we I -+a state that lim f (x) exists, we mean that lim f (x) = L, where L is a real number.) 2. f has a jump discontinuity at a if lim f (x) and lim f (x) bo Time left: Show Time left: Show but lim f (x) f lim f (x) . (Note: When we state that lim f () and