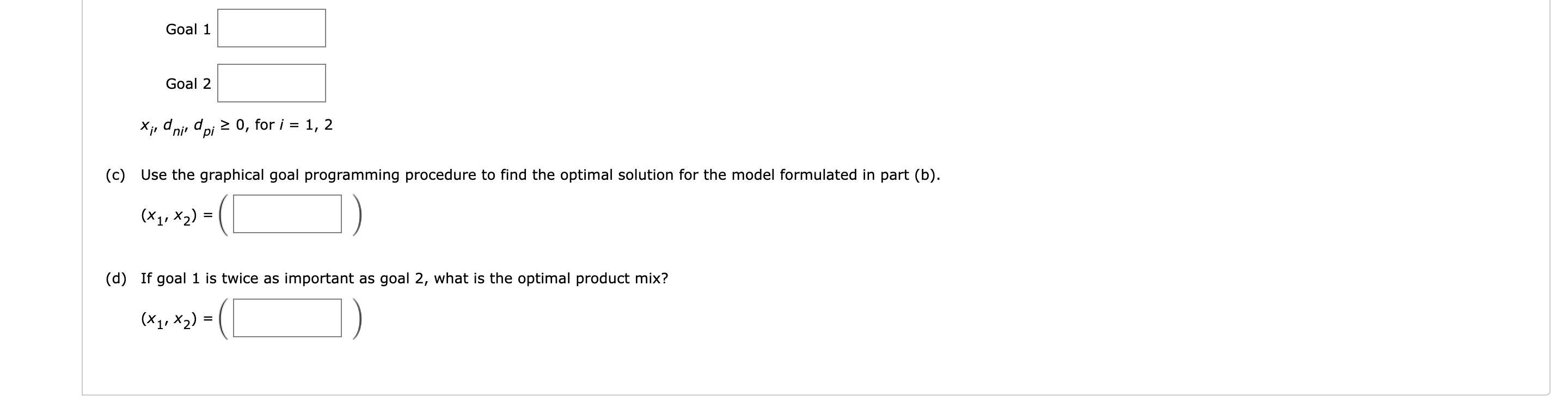
Question: MATH JKP 3 (USE number in this Question and Make answer clear) DO NOT POST IRRELEVANT WORK HERE!!! 3. [-/9.09 Points] DETAILS ASWMSCI15 14.E.001. MY
MATH JKP 3 (USE number in this Question and Make answer clear) DO NOT POST IRRELEVANT WORK HERE!!!

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


