mathlab please write lab report for this problem

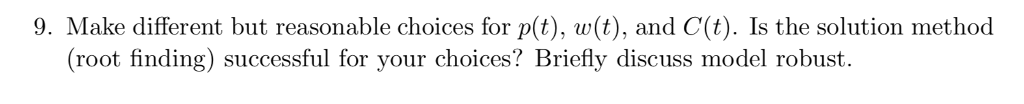
3 Pig Selling Problem Recall the optimization model of maximizing the profit P(t) = p(t)w(t) C(t) from the sale of a pig with weight w(t) in pounds, price p(t) in dollars per pound, and cost of keeping the pig C(t) up to time t in dollars. 5. Write a MATLAB script that uses anonymous functions and the fzero command (or your Newton's method function) to solve the pig selling problem. Specify p(t), w(t), and C(t) along with p'(t), w'(t), and C'(t) at the beginning of the file as function handles and then find t so that p'(t)w(t) + p(t)w'(t) C'(t) = 0. Hint: you will need an anonymous function that combines your other functions like dPdt = @(t) pp (t) *w (t) + p(t) *wp (t) - Cp(t); 6. When should the farmer sell the pig if (as in the textbook, section 1.1), p(t) = 0.65 0.01t, w(t) = 200 + 5t, and C(t) = 0.45t ? 7. When should the farmer sell the pig if (as in the textbook, section 3.1), p(t) = 0.65 0.01t, w(t) = 200 exp(yt), and C(t) = 0.45t? You will need to pick a value of y. Use a nominal value of y = 0.025. Note that the textbook uses the symbol c for y, but that is easy to confuse with C(t). Make a plot of the optimal time to sell ve y for y in the range 0.020 and 0.030. The graph monotonically increases. Explain the meaning of this result. 8. Compute the sensitivity of the optimal time to sell with respect to y (at the nominal value of y). You will need to use a numerical approximation to the derivative