MATLAB CODE without symbolic math toolbox

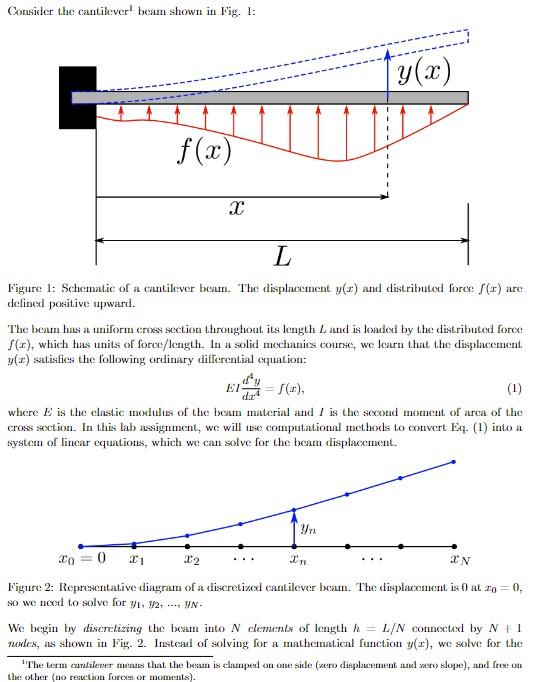
Consider the cantilever 1 beam shown in Fig. 1: Figure 1: Schematic of a cantilever beam. The displacement y(x) and distributed force f(x) are defined positive upward. The beam has a uniform cross section throughout its length L and is loaded by the distributed foroe f(x), which has units of force/length. In a solid mechanics course, we learn that the displacement, y(x) satisfies the following ordinary difterential equation: EIdx4d4y=(x) where E is the elastic modulus of the beam material and I is the socond moment of arca of the cross section. In this lab assignment, we will use computational methods to convert Eq. (1) into a system of linear equations, which we can solve for the beam displacement. Figure 2: Representative diagram of a discretized cantilever beam. The displacement, is 0 at x0=0, so we noed to solve for y1,y2,,yN. We begin by discretizing the beam into N elements of length h=L/N connected by N 1 nodes, as shown in Fig. 2. Instead of solving for a mathematical function y(x), we solve for the 1 The verm cantilewer means that the beam is clamped on one side (zero displacement ambl yero slope), and free on the other (no reaction forces or momunts). displacements at each node: y1=y(x1),y2=y(x2),,yN=y(xN) (note that the displacement. at x0 is prescribed as 0 , so wo only have N unknown displacements). Using methods that we will learn later in this course, it can be shown that the diseretized beam obeys the following system of exuilibrium equations: Ky=f, where? Here, the NN matrix K is known as the stilfness matrix, y is a voctor of unknown displacements, and f is a veetor of preseribed forces. T'he stilfness matrix K hus a tanded structure: all clements are 0 exeept for the five diagonals written above. The discretiand beam is, of coure, an approximation of the continuous besm. The sceuracy of this approximation incresses tis we increas the number of nodes N, but so does the computational cost to solvo tipi. (2). Throughout this assignment, wo will consider a wooden beum with a rectanguhar eroes section, having the following paramecers: For a roctangular cross soction, the socond moment of area I is given by: I=12wd3 Write a MNTLAB function that outputs the NN stiffness matrix K for an arbitrary number of modisN. Part 2: Sinusoidal Loading Using N=64 nodes, compute the displacement, of the beam for the distributed load f(x)=100sin(3L4x)N/m. Plot the undeformed (i.e., a straight line at y=0 ) and deformed shapes of the beam