Matlab Coding . Barycentric Interpolation. There is a function to edit. And a completed code to call the function. There are a few pre-test to make sure program is working properly. I need help recreating/ediitng the function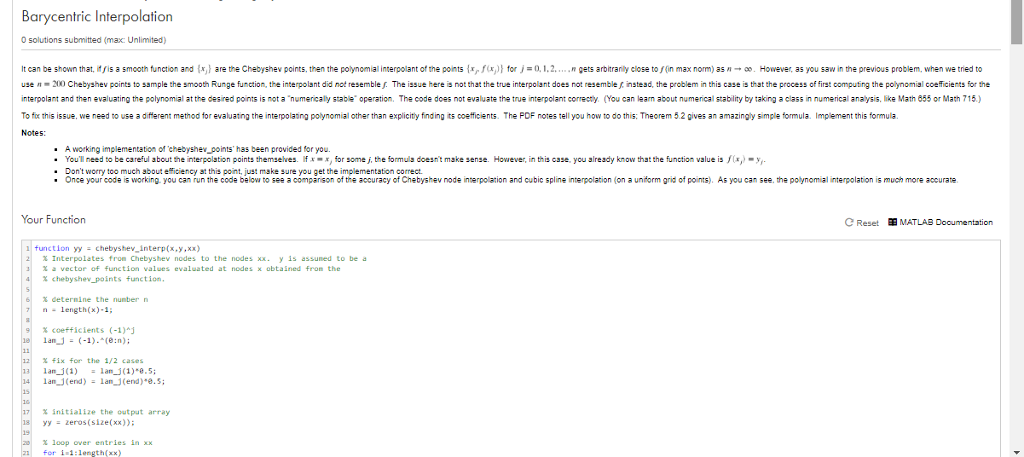

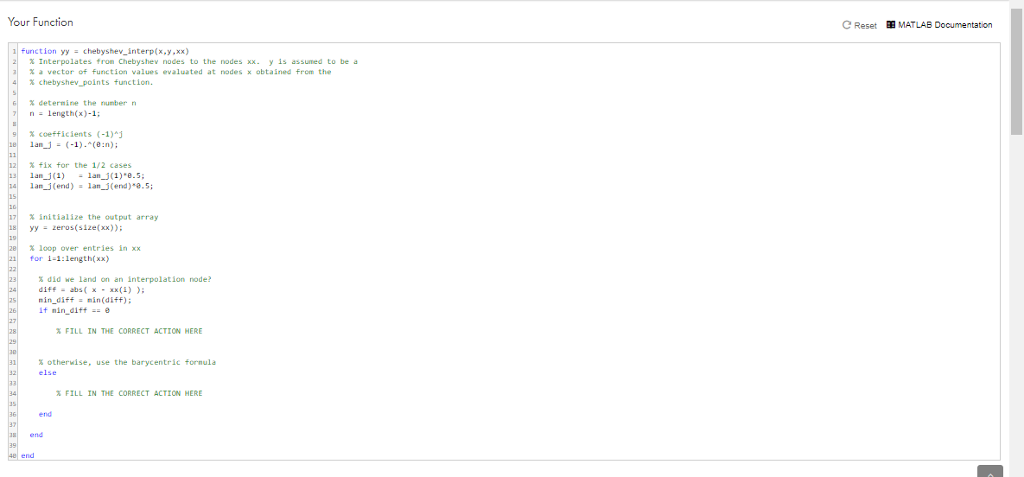
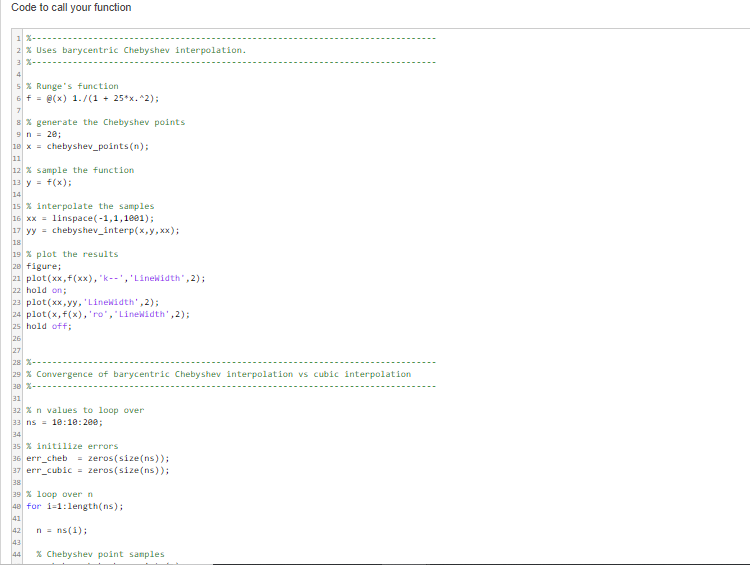
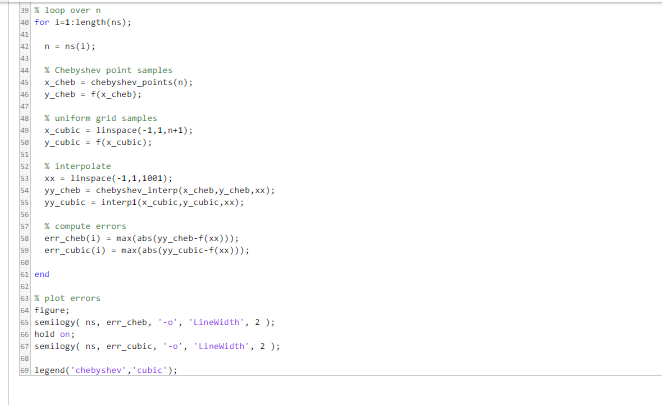
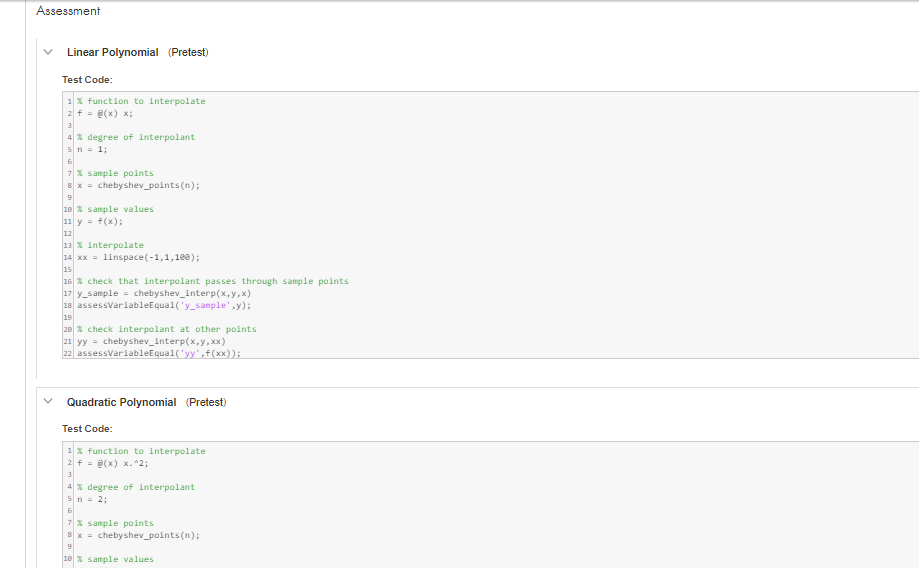
Barycentric Interpolation 0 solutions submitted (max: Unlimited) It can be shown that, i yis a smooth function and lx,) are the Chebyshe points, then the polynomial interpolant of the points fxfor0.1.2... gets arbitranily close to n max norm) asn-. However, as you saw in the previous problem, when we tried to use n-200 Chebyshev points to sample the smooth Runge fumction, the interpolant did not resemble s. The issue here is not that the true interpolant does not resemble instead, the problem in this case is that the process of first computing the polynomisl coeficients for the nterpolant and then evaluating the polynomial at the desired points is not a numerically stable operation, The code does not evaluate the true interpolant correcty. (You can learn about numerical stability by taking a class in numerical analysis, like Math 855 or Math 715) To for this issue, we need to use a different method for evaluating the interpolaing polynomial other than explicitly finding its coefficients. The POF notes tell you how to do this: Theorem 5.2 gives an amazingly simple formula. Implement this formula Notes: A working implementation of chebyshex points' has been provided for you. . You'll need to be careful about the interpolation points themseves. If x,for some j, the formuls doesn't make sense. However, in this case, you slready km.ow that the function value isy Don't worry too much about eFiciency at this point, just make sure you get the implementation correct. Once your code is working you can run the code below to see a comparison of the accuracy of Chebyshev node interpolation and cubic spline interpolation (on a uniform grid of points). As you can see, the polynomial interpolation is much more accurate Your Function C Reset BMATLAB Documentation function yy- chebyshev interp(x,y,xx) % Interpolates fron Chebyshev nodes to the nodes x. y is assumed to be a 3 chebyshe_points function determine the number n n length(x)-1 %coefficients (-1) Ian-J (-1)."(e:n); % fix for the 1/2 cases lamJ(end)lanJ(end).5 % initialize the output array y-zeros(size(xx)) % loop over entries in xx For i 1:length(xx) Barycentric Interpolation 0 solutions submitted (max: Unlimited) It can be shown that, i yis a smooth function and lx,) are the Chebyshe points, then the polynomial interpolant of the points fxfor0.1.2... gets arbitranily close to n max norm) asn-. However, as you saw in the previous problem, when we tried to use n-200 Chebyshev points to sample the smooth Runge fumction, the interpolant did not resemble s. The issue here is not that the true interpolant does not resemble instead, the problem in this case is that the process of first computing the polynomisl coeficients for the nterpolant and then evaluating the polynomial at the desired points is not a numerically stable operation, The code does not evaluate the true interpolant correcty. (You can learn about numerical stability by taking a class in numerical analysis, like Math 855 or Math 715) To for this issue, we need to use a different method for evaluating the interpolaing polynomial other than explicitly finding its coefficients. The POF notes tell you how to do this: Theorem 5.2 gives an amazingly simple formula. Implement this formula Notes: A working implementation of chebyshex points' has been provided for you. . You'll need to be careful about the interpolation points themseves. If x,for some j, the formuls doesn't make sense. However, in this case, you slready km.ow that the function value isy Don't worry too much about eFiciency at this point, just make sure you get the implementation correct. Once your code is working you can run the code below to see a comparison of the accuracy of Chebyshev node interpolation and cubic spline interpolation (on a uniform grid of points). As you can see, the polynomial interpolation is much more accurate Your Function C Reset BMATLAB Documentation function yy- chebyshev interp(x,y,xx) % Interpolates fron Chebyshev nodes to the nodes x. y is assumed to be a 3 chebyshe_points function determine the number n n length(x)-1 %coefficients (-1) Ian-J (-1)."(e:n); % fix for the 1/2 cases lamJ(end)lanJ(end).5 % initialize the output array y-zeros(size(xx)) % loop over entries in xx For i 1:length(xx)