Matlab. Consider the production model x = Cx + d (as explained in Section 2.6 of the textbook) for an economy with C and d as follows (using Matlab notation): C = [.1588 .0064 .0025 .0304 .0014 .0083 .1594; .0057 .2645 .0436 .0099 .0083 .0201 .3413; .0264 .1506 .3557 .0139 .0142 .0070 .0236; .3299 .0565 .0495 .3636 .0204 .0483 .0649; .0089 .0081 .0333 .0295 .3412 .0237 .0020; .1190 .0901 .0996 .1260 .1722 .2368 .3369; .0063 .0126 .0196 .0098 .0064 .0132 .0012]

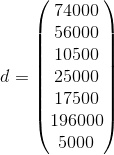d = [74000 56000 10500 25000 17500 196000 5000]

(a) Use Matlab to solve the prediction model x = Cx + d by finding and using an inverse matrix to determine the production level necessary to satisfy the final demand.

(b) Use the iterative approach described in Problem 15 in Section 2.6 of the textbook: Set 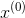= d. Then have Matlab compute 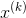= d + C 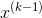for k = 1, 2, . . .. How many iterations are needed before each entry in 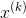is within .01 of the corresponding entry in your answer from part (a)?

For this problem, turn in a diary or script (showing both the Matlabs statements used, and Matlabs output) for parts (a) and (b). Make sure the number of iterations needed is clearly stated in part (b).

1.1588 .0064 .0025 .0304 .0014 .0083 1594 0057 .2645 0436 0099 0083 0201 3413 0264 1506 3557 .0139 .0142 .0070 .0236 C 3299 0565 0495 3636 0204 0483 0649 0089 .0081 .0333 .0295 3412 .0237 0020 1190 0901 0996 1260 1722 2368 .3369 0063 .0126 .0196 .0098 .0064 .0132 .0012