Matlab help (layout already given) (a-c)

(a) Use the reduced row echelon form (RREF) to solve Ax = b, where A and b are indicated in Exercise 1, and type your answer for the following in the Live Editor.

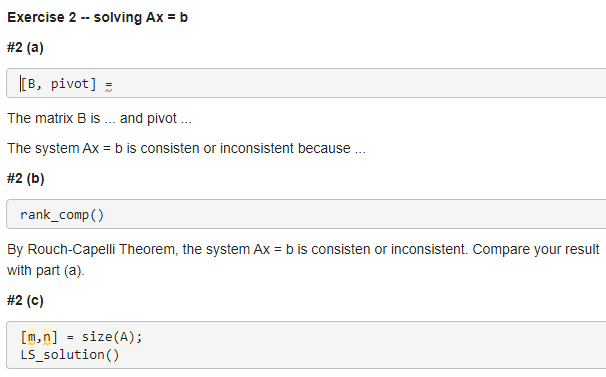
Display the reduced row echelon form and the pivot columns of the augmented matrix [A b].

Write a report in Live Editor to explain if there is a solution of Ax = b.

(b) Verify Rouch-Capelli Theorem by checking the rank(A) and rank([A b]).

Call the function rank_comp and determine if Ax = b is consistent.

Compare the result with part (a)

Note: rank_comp gives you a new command to compare if rank(A) = rank([A b]). When you need to use the command, read the comments in the m-file function first and call the function by typing the name of the function, rank_comp(A,B), in the Live Editor where A and B are the two input matrices.

(c) Open the template LS_solution, and write the code using if-elseif statement (by modifying rank_comp.m). Call LS_solution and display the result for Ax = b as one of the following.

The system Ax = b is inconsistent and it has no solution, or

The system Ax = b is consistent and it has a unique solution, or

The system Ax = b is consistent and it has infinitely many solutions

Note: You should include three inputs (n, A, Ab) for LS_solution, where n is the number of variables in the system of equation.

DISPLAY IN MATLAB

THE 2 M-FILE FUNCTIONS GIVEN

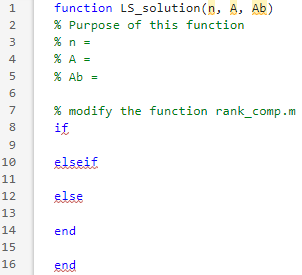
In this exercise, you use RREF and Rouch-Capelli Theorem to determine if Ax=b is consistent. You may need the following commands for this exercise. - The command rref (A) returns the reduced row echelon form of a matrix A - The command [B,pivot]= returns the matrix B=rref(A) and pivot indicates pivot columns - The command rank (A) returns the rank of a matrix A You also need two m-file functions rank_comp (given) and LS_solution (template only). In these functions, you need to know - if-else statement: If expression is true, it executes the statements1 block. Otherwise, it executes the statements2 block. if expression statements1 else statements2 end - if-elseif statement: If expression1 is true, it executes the statements1 block. If not, check expression2. If expression2 is true, it executes the statements 2 block. If not, executes the statements 3 block. if expression 1 statements1 elseif expression 2 statements2 else statements 3 end Exercise 2 - solving Ax=b \#2 (a) [[B,pivot] The matrix B is ... and pivot ... The system Ax=b is consisten or inconsistent because ... \#2 (b) rank_comp() By Rouch-Capelli Theorem, the system Ax=b is consisten or inconsistent. Compare your result with part (a). #2 (c) \[ \begin{array}{l} {[\mathrm{m}, \mathrm{n}]=\operatorname{size}(\mathrm{A})} \\ \text { LS_solution() } \end{array} \] function rank_comp(A, Ab) % Compare the rank of A and its augmented matrix [A b] % A = coefficient matrix of linear equations % Ab = corresponding augmented matrix [A b] if rank(A)==rank(Ab) disp(rank([A]) equals to rank([A b ])) else disp('rank( [A]) does not equal to rank([A b ])) end end function LS_solution( n,A,Ab) % Purpose of this function %n= %A= %Ab= % modify the function rank_comp.m if elseif else end end