Matlab

now pls

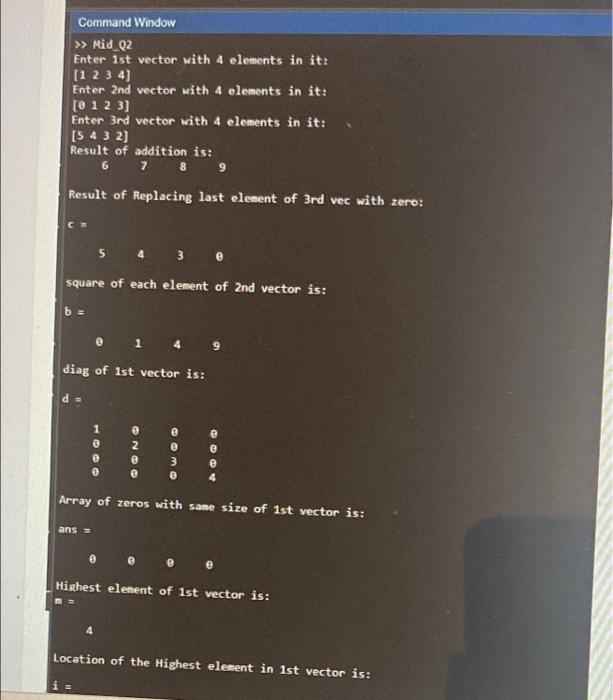
Get 4 vectors of 3 elements each, from the user .1 Add all 4 vectors .2 Replace the first element of the 2 nd vector with zero 3 Display the square of each element in the 3rd vector .4 Use 'diag' to create a matrix with elements of 2nd vector on its main diagonal .5 Create an array of zeros that is the same size of existing 1 st vector 6 Find the highest element in 1 st vector 7 Find the location of the highest element in 1st vector 8 Find the row and column of the highest element in 1 st vector .9 Get a random vector with 3 elements in it and add it with 2 nd vector 10 Calculate the round, ceiling, fix and floor of the existing random vector .11 Get a new (33) matrix from the user. Replace its 2 nd column with 3rd column of 12 existing diagonal matrix Calculate the total time taken by you to input the values in command window and .13 get the result Make sure to include all STRINGS as shown in the output given below. Add/Upload the) (screenshot of your Matlab Code + results here Command Window >> Mid_Q2 Enter 1 st vector with 4 elements in it: [1234] Enter 2nd vector with 4 elements in it: Enter 3rd vector with 4 elements in it: [5432] Result of addition is: 6789 Result of Replacing last elenent of 3rd vec with zero: c= 5430 square of each element of 2nd vector is: b= 0149 diag of 1st vector is: d= 1000020000300004 Array of zeros with sane size of 1 st vector is: ans = Highest element of 1 st vector is: m= 4 Location of the Highest elewent in 1 st vector is: i= Location of the Highest elenent in 1st vector is: I= 4 The randon vector with 4 elenents in it is: e.8147 0.90580.12700.9134 Addition of randon vector with ist vector gives: ans=1.81472.90583.12704.9134 The round of randoe vector is: ans = 1101 The fix of randon vector is: The ceil of randon vector is: ans - 1111 The floor of randon vector is: ans = 0000 Enter a new 44 matrix: Result of Roplacing its 3rd Colunn with 1st colun of existing diagonal matrix: f= \begin{tabular}{llll} 1 & 1 & 0 & 1 \\ 2 & 2 & 0 & 2 \\ \hline \end{tabular}