MATLAB ONLY !!

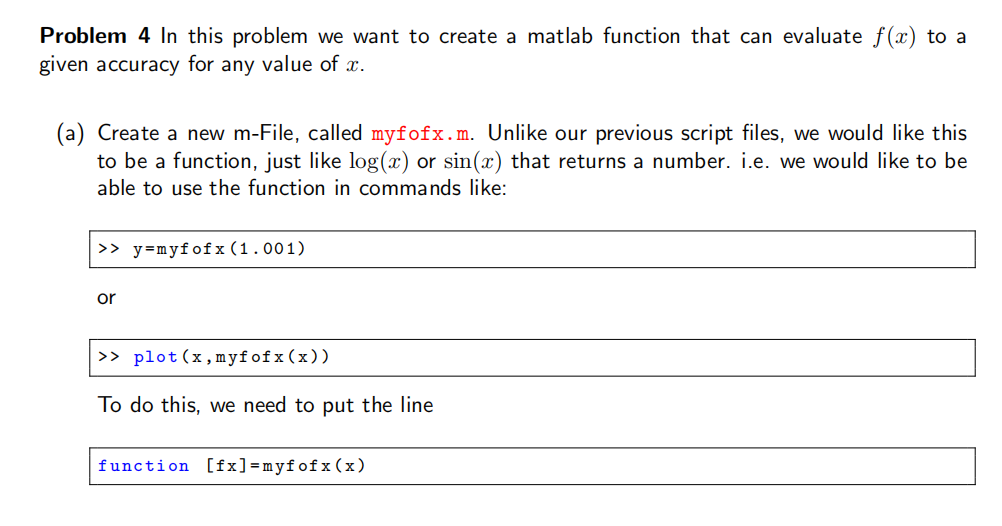
Problem 4 In this problem we want to create a matlab function that can evaluate f(x) to a given accuracy for any value of x. (a) Create a new m-File, called myfofx.m. Unlike our previous script files, we would like this to be a function, just like log(x) or sin(x) that returns a number. i.e. We would like to be able to use the function in commands like: >> y=myfofx (1.001) or >> plot(x,myfofx(x)) To do this, we need to put the line function [fx]=myfofx(x) as the first non-commented line in the m-file. Then, fx will be the variable that we will use in the m-file that, at the end of the calculation, contains our answer. Note that unlike previous cases where x and T were scalars you will not need to set the value of x as it will be passed to the function. In this case, just return the value of the n = 8 Taylor series (i.e. replace the fprintf statement with fx=T before the return). Test the function by evaluating the result on the command line for myfofx(1) and myfofx(2). Make sure you are getting the correct result before proceeding. (b) If we are close to x = 1 our previous results suggest that it would be better to use the Taylor series. However, if we are far away from x = 1, the accuracy of our Taylor series starts to degrade due to truncation error. Use an if-else construct to modify your function to use the Taylor series when 1 10-6 > y=myfofx (1.001) or >> plot(x,myfofx(x)) To do this, we need to put the line function [fx]=myfofx(x) as the first non-commented line in the m-file. Then, fx will be the variable that we will use in the m-file that, at the end of the calculation, contains our answer. Note that unlike previous cases where x and T were scalars you will not need to set the value of x as it will be passed to the function. In this case, just return the value of the n = 8 Taylor series (i.e. replace the fprintf statement with fx=T before the return). Test the function by evaluating the result on the command line for myfofx(1) and myfofx(2). Make sure you are getting the correct result before proceeding. (b) If we are close to x = 1 our previous results suggest that it would be better to use the Taylor series. However, if we are far away from x = 1, the accuracy of our Taylor series starts to degrade due to truncation error. Use an if-else construct to modify your function to use the Taylor series when 1 10-6