MATLAB QUESTION

A hot topic in nanomaterials engineering is the growth of cylindrical nano-sized rods of gold, silver and other plasmonically active materials to be used as nano-antennae, sensor materials and tunable light-emitters in a very wide range of applications. The target properties are achieved by creating very long, thin rods (i.e. l is much larger than 2r, where l is the cylinder length and r is the cylinder radius).

When they are being made, the nano-rods will assume shapes that minimise their total energies at chemical equilibrium in the colloids in which they are grown. The energy of a nano-rod can be approximated by the following proportionality equation:

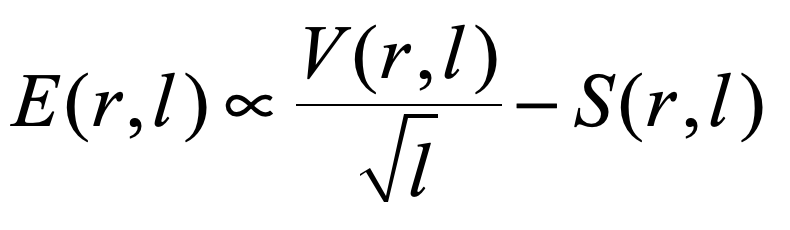
The surface area (S) and volume (V) of a cylindrical rod with radius r, and length l, are given by the following standard equations:

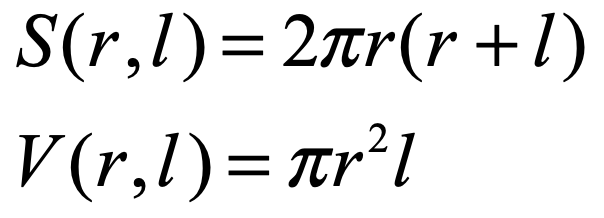
i) You will be creating nanorods with a particular length, and wish to find what the matching radius is for that length. How will you find r_eq?List an ordered set of steps that implement a root-finding procedure to determine the equilibrium radius for your particular length of nanorod.

ii) Determine the value of the equilibrium radii, r_equilibrium, of nano-rods that have grown to a length of l = 5.5 nm in a particular colloid. Give your answer in nm to at least 1 decimal place.

iii) You want to find what values of l will give you the long, thin shape that you desire. Adapting your code from the previous question, write a script that will repeatedly solve for r_equilibrium for different values of l.

The script should then plot a graph of r_equilibrium for values of l that are between 4.5 nm l 500 nm. Plot your graph as a red dashed line, labelling all axes, and using an appropriate resolution to produce a smooth graph.

E(r.) V(r.) - S(r,1) vi S(r,1)=2 r(r +1) V(r,1)= ar?1