MATLAB QUESTION: if you do not have matlab, please do not try to solve

QUESTION:

write a script for the function below that finds zeros of f (x) = sin(x) with various values for the initial guess. Have the output look similar to the chart pictured below

Function:

function [xc,fEvals] = Newton(f,fp,x0,delta,fEvalMax)

% f is a handle to a continuous function f(x) of a single variable.

% fp is a handle to the derivative of f.

% x0 is an initial guess to a root of f.

% delta is a positive real number.

% fEvalsMax is a positive integer >= 2 that indicates the maximum

% number of f-evaluations allowed.

% % Newtons method is repeatedly applied until the current iterate xc

% has the property that |f(xc)|

% after fEvalsMax function evaluations, then xc is the current iterate.

% % fEvals is the number of f-evaluations required to obtain xc.

fEvals = 0;

while (abs(f(x0))>delta)

fEvals =fEvals+1;

xc = x0 - f(x0)/fp(x0);

if fEvals >= fEvalMax

break;

end

x0= xc;

end

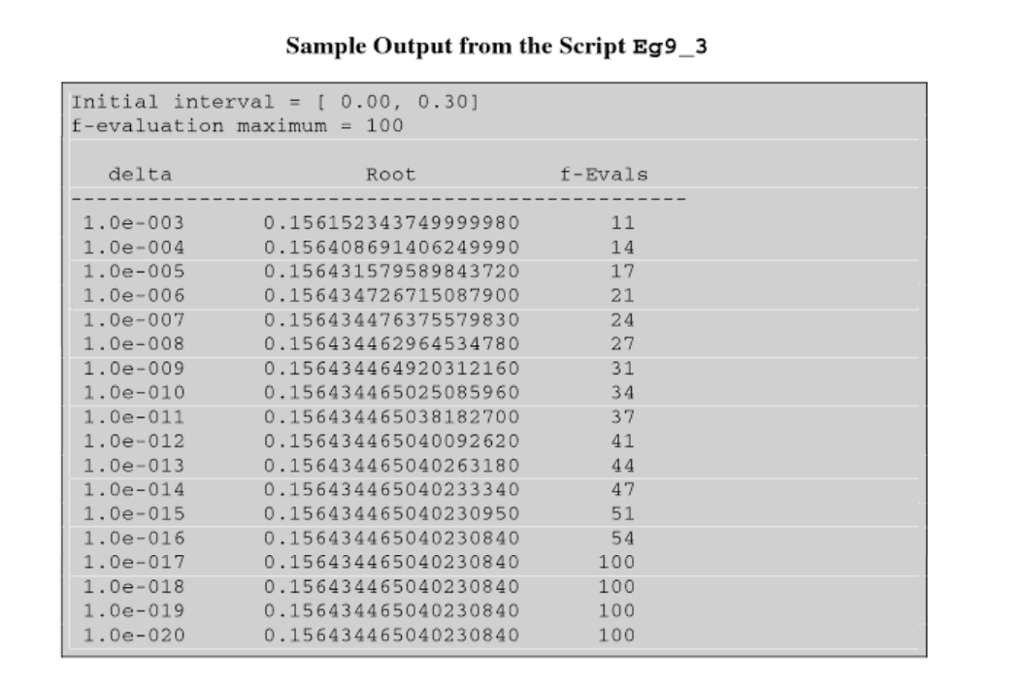
Sample Output from the Script Eg9_3 Initial interval = [ 0.00, 0.30] f-evaluation maximum = 100 delta Root f-Evals 1.0e-003 1.0e-004 1.0e-005 1.0e-006 1.0e-007 1.0e-008 1.0e-009 1.0e-010 1.0e-011 1.0e-012 1.0e-013 1.0e-014 1.0e-015 1.0e-016 1.0e-017 1.0e-018 1.0e-019 1.0e-020 0.156152343749999980 0.156408691406249990 0.156431579589843720 0.156434726715087900 0.156434476375579830 0.156434462964534780 0.156434464920312160 0.156434465025085960 0.156434465038182700 0.156434465040092620 0.156434465040263180 0.156434465040233340 0.156434465040230950 0.156434465040230840 0.156434465040230840 0.156434465040230840 0.156434465040230840 0.156434465040230840 14 17 21 24 27 31 34 37 41 47 51 54 100 100 100 100 Sample Output from the Script Eg9_3 Initial interval = [ 0.00, 0.30] f-evaluation maximum = 100 delta Root f-Evals 1.0e-003 1.0e-004 1.0e-005 1.0e-006 1.0e-007 1.0e-008 1.0e-009 1.0e-010 1.0e-011 1.0e-012 1.0e-013 1.0e-014 1.0e-015 1.0e-016 1.0e-017 1.0e-018 1.0e-019 1.0e-020 0.156152343749999980 0.156408691406249990 0.156431579589843720 0.156434726715087900 0.156434476375579830 0.156434462964534780 0.156434464920312160 0.156434465025085960 0.156434465038182700 0.156434465040092620 0.156434465040263180 0.156434465040233340 0.156434465040230950 0.156434465040230840 0.156434465040230840 0.156434465040230840 0.156434465040230840 0.156434465040230840 14 17 21 24 27 31 34 37 41 47 51 54 100 100 100 100