MATLAB QUESTION: Please do not try to solve if you don't have matlab.

A zero-finding method of great interest is Newtons method. It uses both the value of the function and its derivative at each step. Suppose f and its derivative are defined at xc . (The c is for current.) The tangent line to f at xc has a zero at x+ = xc f (xc )/f (xc) assuming that f(xc) = 0. See Figure 5.4. Newtons method for finding a zero of the function f is based upon the repeated use of this formula.

Complete the following function so that it performs as specified:

function [xc,fEvals] = Newton(f,fp,x0,delta,fEvalMax)

% f is a handle to a continuous function f(x) of a single variable.

% fp is a handle to the derivative of f.

% x0 is an initial guess to a root of f.

% delta is a positive real number.

% fEvalsMax is a positive integer >= 2 that indicates the maximum

% number of f-evaluations allowed.

% % Newtons method is repeatedly applied until the current iterate xc

% has the property that |f(xc)|

% after fEvalsMax function evaluations, then xc is the current iterate.

% % fEvals is the number of f-evaluations required to obtain xc.

Unlike bisection, the Newton process is not guaranteed to terminate. If f (xc) is zero, then the Newton step is not even defined. If f (xc) is small, then a Newton step can take us very far away from a root. Experiment with your implementation by trying to find zeros of f (x) = sin(x) with various values for the initial guess.

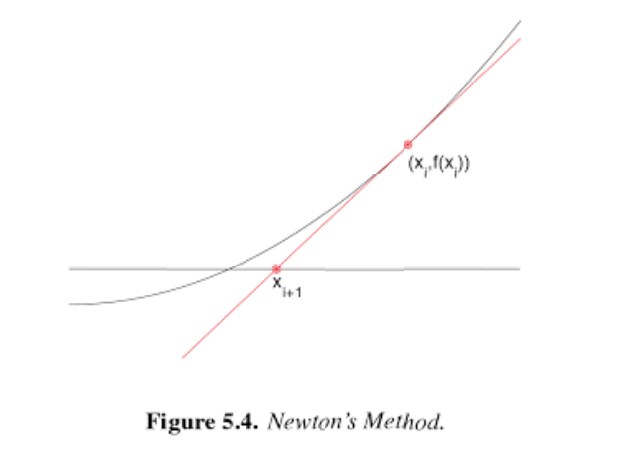
(Xi,f(x)) i+1 Figure 5.4. Newton's Method. (Xi,f(x)) i+1 Figure 5.4. Newton's Method