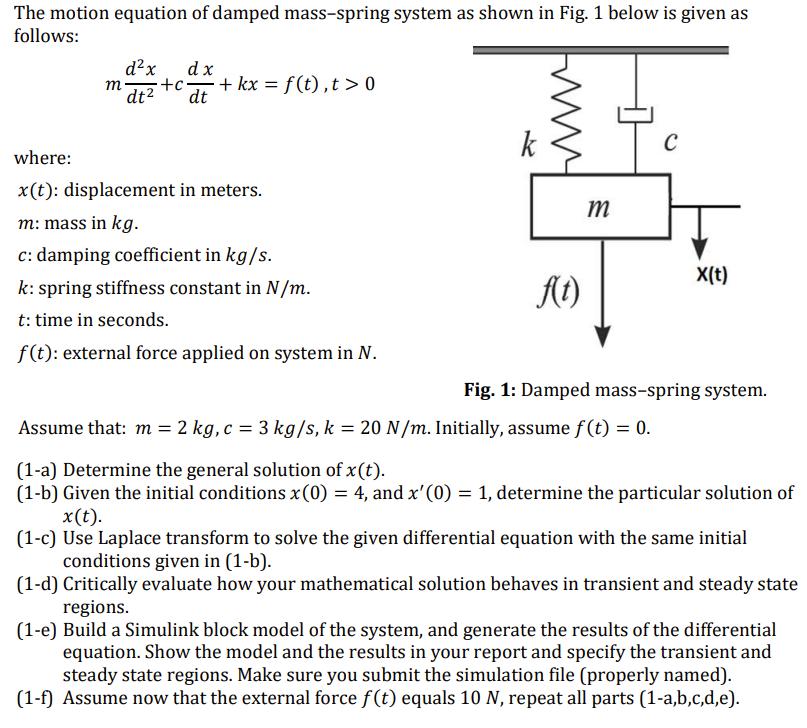
The motion equation of damped mass-spring system as shown in Fig. 1 below is given as follows: dx dx +c dt dt m- + kx = f(t),t> 0 where: x(t): displacement in meters. m: mass in kg. c: damping coefficient in kg/s. k: spring stiffness constant in N/m. t: time in seconds. f(t): external force applied on system in N. k f(t) m C Assume that: m = 2 kg, c = 3 kg/s, k = 20 N/m. Initially, assume f(t) = 0. X(t) Fig. 1: Damped mass-spring system. (1-a) Determine the general solution of x(t). (1-b) Given the initial conditions x (0) = 4, and x'(0) = 1, determine the particular solution of x(t). (1-c) Use Laplace transform to solve the given differential equation with the same initial conditions given in (1-b). (1-d) Critically evaluate how your mathematical solution behaves in transient and steady state regions. (1-e) Build a Simulink block model of the system, and generate the results of the differential equation. Show the model and the results in your report and specify the transient and steady state regions. Make sure you submit the simulation file (properly named). (1-f) Assume now that the external force f(t) equals 10 N, repeat all parts (1-a,b,c,d,e).